Вопрос или проблема
Я пытаюсь понять работу градиентного спуска, стохастического градиентного спуска и градиентного спуска с мини-партиями.
В случае градиентного спуска градиент вычисляется на всем наборе данных на каждом шаге. Я представляю это как несколько задач, где каждая задача рассматривает один элемент из набора данных. В конечном итоге выбирается результат лучшей задачи.
В то время как стохастический градиентный спуск получает новый случайный образец на каждом шаге. Поэтому, в отличие от примера с несколькими задачами выше, есть только одна задача, и на каждом шаге этой задачи выбирается случайный образец. Я предполагаю, что новый случайный образец, который выбирается, должен находиться ниже, чем существующий образец?
В случае градиентного спуска с мини-партиями я представляю это как одну основную задачу, где на каждом шаге возникает несколько задач, в которых каждая задача будет выполнять расчеты градиентной потери, а затем будет взято среднее значение. Затем тот же процесс повторится на следующем шаге.
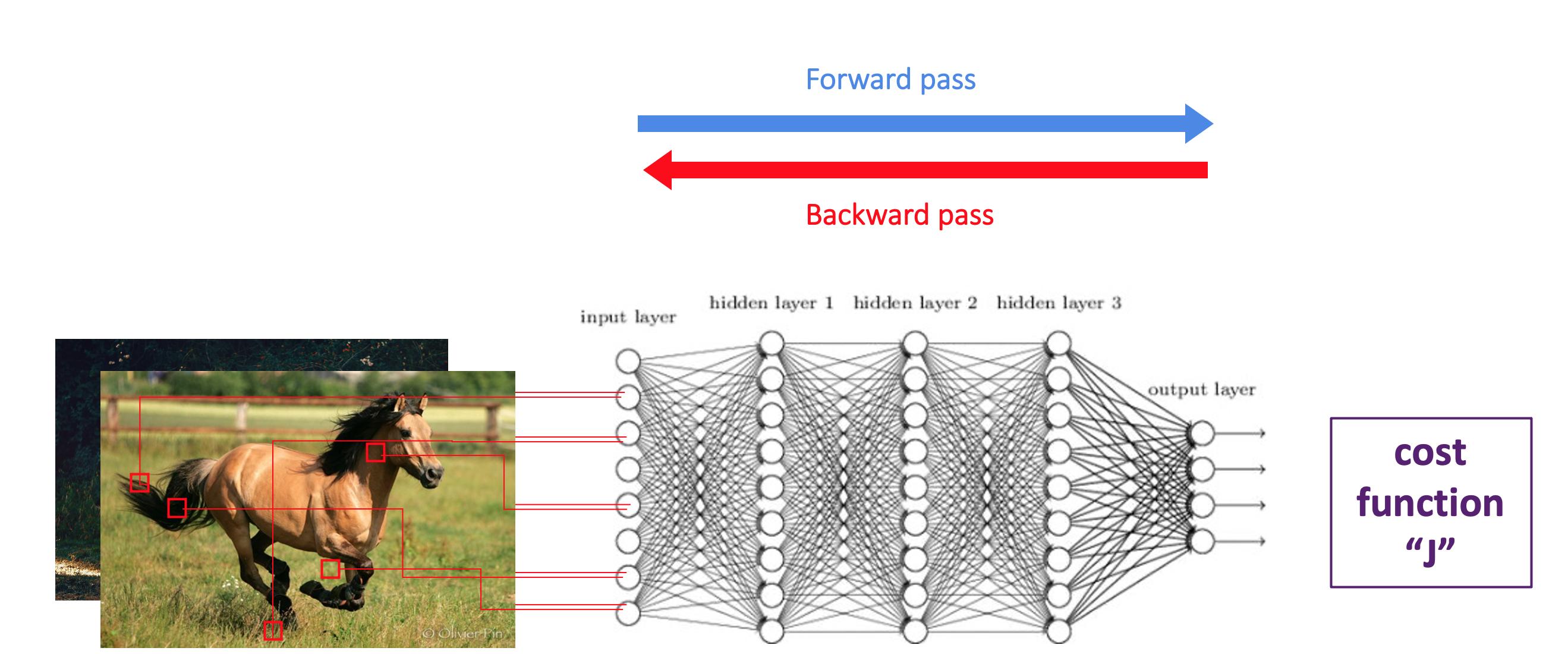
Ваш вопрос тесно связан с тем, как обучаются нейронные сети. Обучение нейронной сети является итеративным. На каждом этапе есть прямой проход и обратный проход.
Прямой проход: вы выбираете партию своих наблюдений и передаете ее нейронным сетям. В процессе прямого прохода ваша нейронная сеть выдает прогнозы и сравнивает их с меткой наблюдений (здесь – животное на картинке). Нейронная сеть затем вычисляет функцию стоимости, что означает среднюю ошибку, совершенную моделью на переданных вами наблюдениях.
Обратный проход: вы будете обновлять различные параметры, начиная с конца и возвращаясь к первым параметрам. Весы будут обновлены с учетом ошибки, которую вы совершили в среднем. После завершения обратного прохода вы можете начать новую итерацию, что означает прямой проход + обратный проход.
Разница между обучением с полными пакетами и мини-пакетами?
Обучение с полными пакетами: как вы сказали, все наблюдения набора данных используются в пакете. Однако они обрабатываются одновременно. Производится уникальный прямой проход и обратный проход. Это достигается с помощью векторизации. Функция стоимости вычисляется как среднее значение ошибок, совершенных на всех наблюдениях.
Обучение с мини-пакетами: вы будете использовать только подмножество ваших наблюдений (скажем, “К”) одновременно. Как только вы выполнили свои прямые и обратные проходы, вы выберете другое подмножество такого же размера (без возможности замены) и сделаете новые итерации. После того, как ваша модель увидит все наблюдения вашего пакета, вы достигли “эпохи“. Затем вы можете начать новую эпоху, перемешав свои наблюдения и создав новые пакеты. Это также называется стохастическим градиентным спуском.
Как выбрать размер пакета?
Это будет зависеть от размера вашего набора данных. При большом размере пакета градиентный спуск является устойчивым, но прямой и обратный проходы медленнее для вычисления. При маленьком размере пакета градиентный спуск будет менее устойчивым, но каждая итерация будет быстрее для вычисления.
Ответ или решение
Понимание Градиентного Спуска: Полный, Стохастический и Мини-Пакетный
Градиентный спуск (GD) является одним из основополагающих методов оптимизации, используемых в машинном обучении и в частности в обучении нейронных сетей. Он позволяет минимизировать функцию потерь путем итеративного обновления параметров модели. Существует несколько вариантов этого метода: полный градиентный спуск (Batch Gradient Descent), стохастический градиентный спуск (Stochastic Gradient Descent) и мини-пакетный градиентный спуск (Mini-Batch Gradient Descent). Важно понимать, как они работают, чтобы правильно применять эти методы в практических задачах.
1. Полный градиентный спуск
Принцип работы:
Полный градиентный спуск рассчитывает градиент функции потерь, используя весь набор данных на каждой итерации. Этот метод требует вычисления полной статистики на всех данных, чтобы корректно обновить параметры модели.
Пример:
Представьте, что у вас есть задача предсказания веса животного на основе его характеристик. Для полного градиентного спуска вы будете брать все данные о животных, вычислять предсказания для каждого из них, сравнивать их с реальными значениями, а затем обновлять веса модели на основе среднего градиента, определенного для всего набора данных.
Преимущества:
- Стабильный и надежный, так как учитывает всю информацию из набора данных.
- Часто дает лучшую оценку параметров.
Недостатки:
- Высокая вычислительная интенсивность, особенно на больших наборах данных.
- Долгое время обработки каждой итерации.
2. Стохастический градиентный спуск
Принцип работы:
Стохастический градиентный спуск вычисляет градиент функции потерь, используя только один случайный элемент из набора данных на каждой итерации. Это создает определенную "шумность" в процессах обучения, что может помочь избежать локальных минимумов, но также может приводить к колебаниям в ходе адаптации параметров.
Пример:
У той же модели предсказания веса животного на каждой итерации вы будете случайным образом выбирать одно животное, вычислять его предсказание и обновлять веса модели на основе этого одного примера. Результаты могут значительно варьироваться от итерации к итерации.
Преимущества:
- Быстрота обновлений параметров — позволяет значительно ускорить процесс.
- Более частые обновления позволяют лучше адаптироваться к изменению данных.
Недостатки:
- Колебания в градиенте могут привести к менее стабильному обучению.
- Может потребоваться больше итераций для достижения сходимости.
3. Мини-пакетный градиентный спуск
Принцип работы:
Мини-пакетный градиентный спуск является компромиссом между полным и стохастическим градиентным спусками. Он использует небольшие подмножества данных (миниквантов, например, размером 32 или 64) на каждой итерации для вычисления градиента.
Пример:
В моделировании веса животных вы могли бы разбить данные на небольшие мини-пакеты по 32 примера худших предсказаний. На каждой итерации вы будете использовать один из пакетов, вычислять предсказания и соответственно обновлять параметры модели.
Преимущества:
- Более стабильный процесс обучения по сравнению со стохастическим градиентным спуском, меньше колебаний.
- Быстрее работает, чем полный градиентный спуск, особенно на больших данных.
- Снижает риск переобучения, обеспечивая обновление на основе нескольких примеров.
Недостатки:
- Оптимальный выбор размера мини-пакета может зависеть от конкретной задачи и размеров данных.
- Если размер мини-пакета слишком мал, можно потерять информацию при обновлениях.
Итог
Градиентный спуск, стохастический градиентный спуск и мини-пакетный градиентный спуск обеспечивают различные подходы к обучению моделей. Полный градиентный спуск обеспечивает стабильные, но неэффективные вычисления; стохастический спуск предлагает быстрые, но менее стабильные обновления; мини-пакетный градиентный спуск сочетает быстроту и стабильность. Выбор подходящего метода зависит от размера вашего набора данных, времени, доступного для вычислений, и требований к точности модели.