Вопрос или проблема
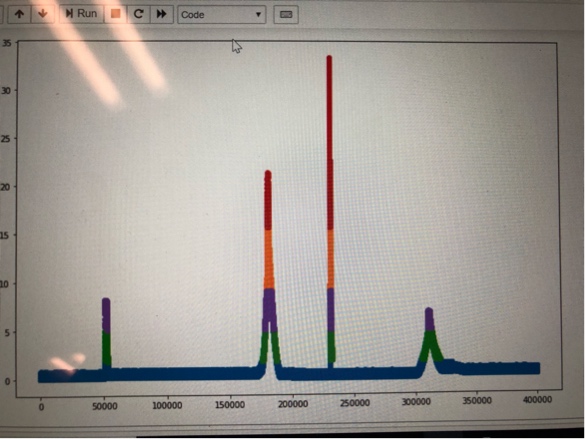
У меня есть остатки многомерных временных рядов, полученные с датчиков на сервере. Всплески на графиках остатка указывают на аномальное состояние сервера. Я хочу сгруппировать данные по вертикальным кластерам и получить индексы точек в каждом кластере, чтобы я мог вернуться и посмотреть на фактические данные и получить средние значения различных параметров кластера.
Я пробовал 1D гауссову класификацию, K-means и т.д., но, похоже, они все группируют данные горизонтально.
Я хочу, чтобы каждый всплеск был отдельным кластером и получить индексы значений в кластере. Может кто-нибудь предложить технику для решения этой проблемы? Спасибо.
Вам могут подойти более полезные методы, если вы будете искать обнаружение событий или обнаружение выбросов, а не кластеризацию. Учитывая форму всплесков в данных, вы можете попробовать использовать среднее значение временного ряда в качестве порога, тогда смежные группы значений, которые превышают глобальное среднее, будут вашими аномальными состояниями. Хотя этот метод может быть немного хрупким в долгосрочной перспективе, поэтому вы можете сделать его более совершенным. Вы можете использовать среднее значение по большому скользящему окну вместо глобального среднего, если вас больше интересуют локальные изменения.
Если вы хотите сохранить концепцию кластеризации, тогда может быть лучше провести кластеризацию в 2D, т.е. ваши точки будут представлять собой кортежи/векторы (время, значение), а не проводить кластеризацию на 1D данных. Другой метод, который, вероятно, сработает, это использовать кластеризацию K-средних на 1D данных, но иметь только 2 кластера (нормальный и аномальный). Затем вам нужно будет использовать информацию о времени для разделения отдельных событий/аномалий.
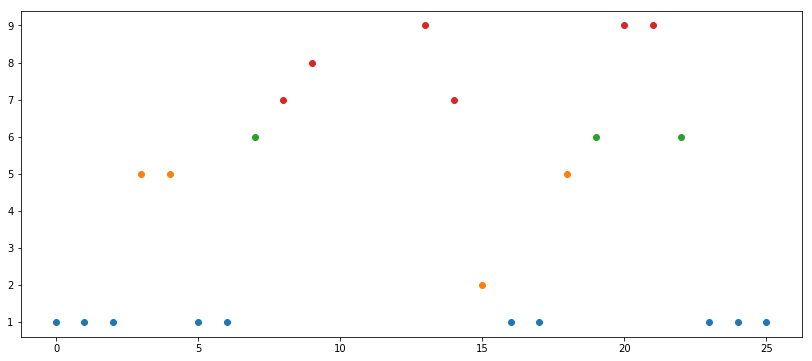
Предполагая, что вы имеете в виду кластеры как цвета на вашем графике, это в основном.percentiles, т.е. сколько точек выше или ниже определенного процента данных.
Чтобы найти точки в вертикальном диапазоне, вам просто нужно найти точки между двумя процентилями. Например, с помощью numpy можно сделать следующее:
a = np.array([1, 1, 1, 5, 5, 1, 1, 6, 7, 8, 10, 13, 10, 9, 7, 2, 1, 1, 5, 6, 9, 9, 6, 1, 1, 1])
a1 = a[(a >= np.percentile(a, 0)) & (a <= np.percentile(a, 25))]
a2 = a[(a > np.percentile(a, 25)) & (a <= np.percentile(a, 50))]
a3 = a[(a > np.percentile(a, 50)) & (a <= np.percentile(a, 65))]
a4 = a[(a > np.percentile(a, 65)) & (a <= np.percentile(a, 80))]
a5 = a[(a > np.percentile(a, 80)) & (a <= np.percentile(a, 90))]
a6 = a[(a > np.percentile(a, 90)) & (a <= np.percentile(a, 100))]
Это дает точки следующим образом:
a1содержит точки в пределах 0-го процентиля (включительно) до 25-го процентиля (включительно)a2содержит точки в пределах 25-го (исключительно) до 50-го (включительно)a3содержит точки в пределах 50-го (исключительно) до 65-го (исключительно)- и так далее
Вам нужно быть осторожным с сравнением (больше чем против больше чем или равно), чтобы включить все точки: один из диапазонов должен быть включен с обеих сторон.
Мы также можем это нарисовать, чтобы увидеть, как это выглядит:
x = np.arange(len(a))
fig, ax = plt.subplots(figsize=(14, 6))
ax.plot(x[np.isin(a, a1)], a1, 'o')
ax.plot(x[np.isin(a, a2)], a2, 'o')
ax.plot(x[np.isin(a, a3)], a3, 'o')
ax.plot(x[np.isin(a, a4)], a4, 'o')
ax.plot(x[np.isin(a, a5)], a5, 'o')
Процентиль — это статистическая мера по умолчанию. Они не являются фиксированными числами. Я использовал очень разные процентильные значения, потому что хотел (1) получить красивые цвета на графике и (2) иметь хотя бы один пустой диапазон (обратите внимание, что a5 пуст, так как между 80-м и 90-м процентилями нет точек). В реальном сценарии лучше брать очень регулярные диапазоны, например, (0, 25, 50, 75, 100) или (0, 10, 20, 30, 40, 50, 60, 70, 80, 90).
Ответ или решение
Как найти вертикальные кластеры в однопредельных данных
При анализе аномальных состояний сервера,огенерированных датчиками, важно обнаружить резкие колебания в резидуа, которые указывают на исключительные ситуации. Эти колебания можно метить как "спайки", и задача заключается в том, чтобы идентифицировать их как отдельные кластеры. Стандартные методы кластеризации, такие как K-means и однопараметрическая Гауссовская модель, зачастую не подходят для этой задачи, так как они не учитывают вертикальные параметры. Рассмотрим более детально, как можно решить эту задачу, используя различные подходы.
1. Обнаружение событий и аномалий
Прежде всего, возможно, вам стоит рассмотреть методы, которые более направлены на выявление событий или аномалий, чем на обычную кластеризацию. Рассмотрим следующие подходы:
-
Аномальная детекция на основе порогового значения: Это может быть достигнуто путем определения порога на основе среднего значения данных. К примеру, вы можете выбрать среднее значение на глобальном или локальном (скользящем) уровне, а затем выделить данные, превышающие этот порог. Каждая последовательная группа точек, превышающая порог, может представлять собой отдельный кластер.
-
Локальное скользящее среднее: Вместо глобального среднего можно использовать локальное среднее – это даст возможность учитывать изменения в данных во времени.
2. Кластеризация в двухмерном пространстве
Хотя в вашем запросе речь идет о 1D данных, переход к 2D пространству может быть полезным. Зафиксируйте точки в виде векторов (время, значение), что поможет K-means или другим методам кластеризации более эффективно выделять вертикальные кластеры.
import numpy as np
import matplotlib.pyplot as plt
# Пример данных
residuals = np.array([...]) # ваш массив резидуума
# Генерация (время, значение)
time = np.arange(len(residuals))
data_points = np.column_stack((time, residuals))
# Применение K-means
from sklearn.cluster import KMeans
kmeans = KMeans(n_clusters=2)
kmeans.fit(data_points)
labels = kmeans.labels_
# Визуализация
plt.scatter(data_points[:, 0], data_points[:, 1], c=labels)
plt.xlabel("Время")
plt.ylabel("Значение")
plt.title("Кластеры")
plt.show()3. Использование percentiles для выделения диапазонов
Процесс выделения кластеров может быть также оптимизирован, используя статистические меры, такие как перцентили. Сначала можно вычислить перцентили и выделить точки внутри заданных диапазонов, что позволит вам структурировать данные в группы в зависимости от их вертикального положения.
percentile_thresholds = np.percentile(residuals, [0, 25, 50, 75, 100])
clusters = [residuals[(residuals > lower) & (residuals <= upper)] for lower, upper in zip(percentile_thresholds[:-1], percentile_thresholds[1:])]
for i, cluster in enumerate(clusters):
print(f"Кластер {i}: индексы = {np.where(np.isin(residuals, cluster))[0]}")Заключение
Чтобы успешно выделить вертикальные кластеры в однопредельных данных, стоит рассмотреть методы детекции аномалий и событий, использовать 2D представление данных для более точной кластеризации, а также применить статистические перцентили для выделения качественных групп. Применяя эти техники в сочетании, вы сможете эффективно анализировать аномальные состояния вашего сервера и возвращаться к соответствующим данным для дальнейшего анализа.