- Вопрос или проблема
- Ответ или решение
- Почему использование градиентного спуска (Gradient Descent) вместо стохастического градиентного спуска (Stochastic Gradient Descent) улучшает производительность
- 1. Определение и принципы работы
- 2. Преимущества GD над SGD
- 3. Устойчивость к переобучению
- 4. Параметры модели и их влияние
- 5. Практическое применение и масштабируемость
- Заключение
Вопрос или проблема
В настоящее время я провожу два типа логистической регрессии.
- логистическая регрессия с использованием стохастического градиентного спуска (SGD)
- логистическая регрессия с использованием градиентного спуска (GD)
реализовано следующим образом
SGD= SGDClassifier(loss="log",max_iter=1000,penalty='l1',alpha=0.001)
logreg = LogisticRegression(solver="liblinear", max_iter=100, penalty='l1', C=0.1)
не обращайте внимания на гиперпараметры, так как я использовал GridsearchCV и пробовал разные комбинации.
При расчете точности логистическая регрессия с GD показывает лучшие результаты, чем с SGD. Я хочу понять, почему это так, является ли использование GD вместо SGD одним из способов смягчения недообучения модели?
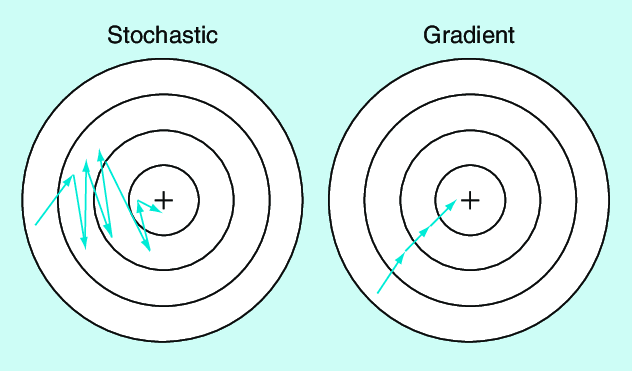
SGD имеет эффект регуляризации и находит решение быстрее. GD, с другой стороны, рассматривает все данные и находит следующий лучший шаг.
SGD может прийти к оптимальному глобальному минимуму, но GD может. Но GD не практичен для больших данных.
Градиентный спуск должен показывать лучшие результаты, так как он работает с вашими полными данными.
Стохастический градиентный спуск рассматривает батчи, что делает его полезным для больших данных. Батчи (или подмножества) позволяют работать быстрее, но он может сосредоточиться на локальном минимуме.
На Википедии вы можете найти следующее цитату:
SGD заменяет реальный градиент (вычисленный по всему набору данных) его оценкой (вычисленной по случайно выбранному подмножеству данных). Особенно в задачах оптимизации с высокой размерностью это снижает вычислительную нагрузку, достигая более быстрых итераций в обмен на более низкую скорость сходимости.
Ответ или решение
Почему использование градиентного спуска (Gradient Descent) вместо стохастического градиентного спуска (Stochastic Gradient Descent) улучшает производительность
В данной статье мы рассмотрим различия между градиентным спуском (GD) и стохастическим градиентным спуском (SGD), а также обсудим причины, по которым использование GD может привести к лучшим результатам в контексте логистической регрессии.
1. Определение и принципы работы
-
Градиентный спуск (GD): Это метод оптимизации, который использует весь набор данных для вычисления градиента функции ошибки. GD обновляет параметры модели после полного прохода по данным, что обеспечивает высокую точность градиента и может гарантировать достижение глобального минимума для выпуклых функций.
-
Стохастический градиентный спуск (SGD): Вместо использования всего набора данных, SGD обновляет параметры на основе оценки градиента, рассчитанного по случайной подвыборке (или отдельному примеру). Это уменьшает вычислительные затраты и позволяет получить более быстрые итерации, но может привести к переходу в локальные минимумы из-за шума в оценках градиента.
2. Преимущества GD над SGD
-
Точность и стабильность: Поскольку GD использует все данные для вычисления градиента, он обладает более высокой стабильностью и точностью. Это означает, что он более вероятно приведет к обнаружению более оптимального решения, особенно если модель подвержена переобучению или имеет сложную зависимость между признаками.
-
Конвергенция к глобальному минимуму: GD имеет возможность конвергировать к глобальному минимуму для выпуклых функций, что может быть особенно важно для логистической регрессии, где точность предсказаний критична. В то же время SGD, будучи подверженным шуму, может "столкнуться" с локальными минимумами, что увеличивает риск недообучения.
3. Устойчивость к переобучению
Хотя SGD часто используется для повышения устойчивости модели за счет регуляризации, GD может лучше справляться с моделями, которые имеют сложные отношения между переменными. Это может привести к более точным предсказаниям на тестовых данных, особенно если использованные гиперпараметры были подобраны правильно с помощью методов, таких как GridSearchCV.
4. Параметры модели и их влияние
Значения параметров, таких как регуляризация (penalty), размеры итераций (max_iter), и коэффициенты обучения (alpha, C), могут значительно повлиять на производительность как GD, так и SGD. В вашем случае вы упомянули регуляризацию L1, которая может способствовать уменьшению переобучения и созданию более интерпретируемых моделей.
5. Практическое применение и масштабируемость
Хотя GD может демонстрировать лучшую производительность с точки зрения точности, он требует больше вычислительных ресурсов и времени при работе с большими объемами данных. Этот аспект делает SGD предпочтительным для задач, связанных с большими данными, несмотря на его недостатки в точности.
Заключение
Использование градиентного спуска по сравнению со стохастическим градиентным спуском действительно может привести к более высокой производительности модели в задачах логистической регрессии. GD обеспечивает более точные и стабильные обновления параметров, что может быть критически важным для достижения хороших результатов, особенно в сложных сценариях. Тем не менее, выбор метода оптимизации должен основываться на конкретных условиях задачи, включая размер данных и вычислительные ресурсы.