Вопрос или проблема
Известно, что итерация SGD имеет большую дисперсию.
Учитывая обновление итерации:
$$
w^{k+1} := w^k – \underbrace{\alpha \ g_i(w^k)}_{p^k},
$$
где $w$ – веса модели, а $g_i(w^k)$ – градиент функции потерь, оцененный для образца $i$. Как я могу вычислить дисперсию каждого обновления $p^k$?
Я хотел бы построить график для каждой итерации и изучить его поведение в процессе минимизации.
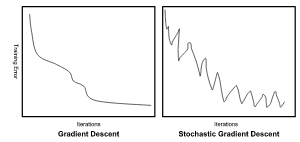
Вы можете построить график обновления по сравнению с итерацией и проанализировать изменения каждого обновления по мере увеличения числа итераций. Как здесь здесь, где они сравнивают дисперсию стандартного алгоритма градиентного спуска с его стохастической версией.
Ответ или решение
Для вычисления дисперсии обновления в итерации стохастического градиентного спуска (SGD) необходимо внимательно рассмотреть природу обновления весов модели, заданного формулой:
$$
w^{k+1} := w^k – \underbrace{\alpha \ gi(w^k)}{p^k}.
$$
Здесь (w) представляет собой веса модели, (\alpha) — скорость обучения, а (g_i(w^k)) — градиент функции потерь, вычисленный для конкретного образца (i). Основное преимущество SGD заключается в его способности использовать только один образец (или небольшую партию образцов), что приводит к более быстрой обработке данных по сравнению с полным градиентным спуском (BGD). Однако из-за такой выборки SGD обычно сопровождается высокой дисперсией.
Шаги для вычисления дисперсии обновления (p^k)
-
Определение (p^k):
Обновление весов в SGD обозначается как (p^k = -\alpha g_i(w^k)). Важно отметить, что это обновление зависит от конкретного (случайного) образца (или мини-парти). -
Компьютирование матожидания градиента:
Предположим, что у нас есть выборка из (N) образцов, и градиент для образца (i) можно рассматривать как случайную величину. Для вычисления дисперсии нам нужно определить математическое ожидание градиента:
$$
\mathbb{E}[g(w^k)] = \frac{1}{N} \sum_{j=1}^N g_j(w^k),
$$
где (g_j(w^k)) — это градиент для образца (j). -
Вычисление дисперсии (g_i(w^k)):
Дисперсия градиента для избранного образца (i) может быть найдена следующим образом:
[
\text{Var}(g_i(w^k)) = \mathbb{E}[g_i^2(w^k)] – \left(\mathbb{E}[g_i(w^k)]\right)^2.
]
Здесь (\mathbb{E}[g_i^2(w^k)]) — это математическое ожидание квадратов градиента для образца (i), а (\mathbb{E}[g_i(w^k)]) — это уже определенное математическое ожидание градиента. -
Дисперсия обновления (p^k):
Теперь можно вычислить дисперсию обновления (p^k):
[
\text{Var}(p^k) = \alpha^2 \text{Var}(g_i(w^k)).
]
Это связано с тем, что (\alpha) — это фиксированное значение, и при вычислении дисперсии константа возводится в квадрат. -
Построение графика:
Для анализа поведения дисперсии обновлений в ходе минимизации функции потерь можно построить график значений дисперсии на каждой итерации. В этом графике по оси (x) будут изображены итерации, а по оси (y) — значения дисперсии (Var(p^k)). Это даст понимание того, как изменяется дисперсия при увеличении числа итераций.
Заключение
Понимание и вычисление дисперсии в стохастическом градиентном спуске критически важно для оценки стабильности и эффективности алгоритма. Высокая дисперсия может приводить к неустойчивым обновлениям весов и замедлению сходимости. С помощью полученных формул можно проанализировать, как различные параметры, такие как скорость обучения и размер выборки, влияют на результаты обновлений, что поможет в тонкой настройке модели.