Вопрос или проблема
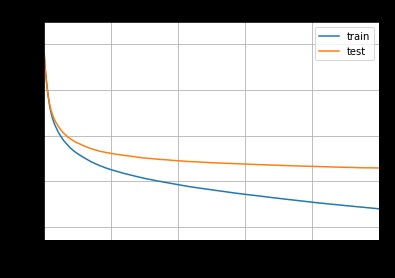
Я запустил модель линейной регрессии lighgbm, оптимизируя по RMSE и измеряя производительность по RMSE:
model = LGBMRegressor(objective="regression", n_estimators=500, n_jobs=8)
model.fit(X_train, y_train, eval_metric="rmse", eval_set=[(X_train, y_train), (X_test, y_test)], early_stopping_rounds=20)
Модель продолжает улучшаться в течение 500 итераций. Вот результаты, которые я получаю по MAE:
MAE на обучающей выборке: 1.080571
MAE на тестовой выборке: 1.258383
Но метрика, которая мне действительно интересна, это MAE, поэтому я решил оптимизировать ее напрямую (и выбрать ее в качестве метрики оценки):
model = LGBMRegressor(objective="regression_l1", n_estimators=500, n_jobs=8)
model.fit(X_train, y_train, eval_metric="mae", eval_set=[(X_train, y_train), (X_test, y_test)], early_stopping_rounds=20)
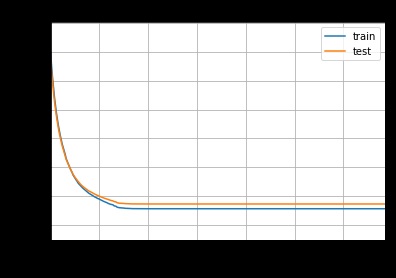
Наперекор всем ожиданиям, производительность MAE снижается как на обучающей, так и на тестовой выборках:
MAE на обучающей выборке: 1.277689
MAE на тестовой выборке: 1.285950
Когда я смотрю на логи модели, кажется, что она застряла в локальном минимуме и не улучшает результаты после примерно 100 деревьев… Думаете, что проблема связана с недифференцируемостью MAE?
Вот кривые обучения:
Мое предположение заключается в том, что это связано с различиями между двумя мерами: по сравнению с MAE, RMSE придает большее значение большим ошибкам из-за квадрата. В результате модель, оптимизированная по RMSE, имеет сильный стимул корректировать свои предсказания, когда они сильно отклоняются от истинного значения, даже если такие случаи не часты. В то время как модель, оптимизированная по MAE, склонна отдавать предпочтение получению правильного предсказания для как можно большего числа экземпляров.
Таким образом, моя гипотеза заключается в том, что модель, оптимизированная по RMSE, находит лучшие параметры, пытаясь сначала решить большие ошибки, тогда как модель, оптимизированная по MAE, оказывается в состоянии, когда она не может улучшить результаты по нескольким случаям с большими ошибками, не жертвуя многими случаями с маленькой ошибкой. Это должно быть возможно проверить, наблюдая, какие экземпляры две модели предсказывают по-разному и насколько.
Я также отмечу, что модель, оптимизированная по MAE, не переобучается так сильно, как модель, оптимизированная по RMSE. Поэтому я не уверен, что модель RMSE в целом гораздо лучше, чем модель MAE, учитывая, что разница в производительности на тестовой выборке не так велика.
Действительно, оптимизация функции стоимости MAE представляет собой ряд проблем в моделях на основе бустинга, потому что эта функция стоимости не является дважды дифференцируемой. Более того, время вычислений может значительно увеличиваться.
В Xgboost оптимизация MAE стала возможной еще с версии 1.7.0 (ноябрь 2022 года), но нам пришлось подождать несколько исправлений ошибок и версию 2.0 (июль 2023 года), прежде чем это заработало (https://github.com/dmlc/xgboost/issues/7674).
Наконец, еще одной альтернативой может быть подгонка модели под квадратный корень от меток, а затем квадратирование предсказаний. Для получения дополнительной информации смотрите этот ноутбук на Kaggle: https://www.kaggle.com/code/theudbald/optimize-mean-asolute-error-mae-with-xgboost)
Ответ или решение
Оптимизация MAE и ухудшение метрик MAE
Оптимизация модели с использованием метрик, таких как MAE (средняя абсолютная ошибка), может быть сложной задачей, особенно в контексте градиентного бустинга. В вашем случае вы провели два эксперимента: первый с оптимизацией по RMSE (средняя квадратичная ошибка), а второй – по MAE. В результате вы заметили, что при оптимизации MAE метрика ухудшается, несмотря на то, что вы ожидаете обратное. Давайте разберёмся в возможных причинах этого явления.
1. Разница в метриках
Ваше наблюдение о том, что RMSE отдает предпочтение большим ошибкам, совершенно верно. RMSE имеет свойство "наказывать" большие ошибки, поскольку они возводятся в квадрат. Это может привести к тому, что модель, оптимизируемая по RMSE, становится более чувствительной к редким, но значительным отклонениям, а также пытается скорректировать их, что может улучшить общие предсказания, даже если средние ошибки остаются менее приемлемыми.
С другой стороны, MAE рассматривает все отклонения на равных основаниях и стремится минимизировать среднее абсолютное значение ошибок. Таким образом, модель, оптимизируемая по MAE, может искать компромиссы и в некоторых случаях "застревать" в локальных минимумах, не в состоянии улучшить предсказания по отдельным, более значительным ошибкам без ущерба для других.
2. Непрерывность и дифференцируемость функции потерь
Основная причина затруднений при оптимизации MAE может быть связана с тем, что эта функция потерь является не дифференцируемой вдоль оси нуля. Это делает невозможным применение градиентного спуска в традиционном его понимании, поскольку нет единственной предопределенной производной. В результате, модули градиентного бустинга, такие как LightGBM, могут слишком рано терять способность к обучению и застрять на местных минимумах. Это видно и в ваших логах, где модель не улучшает результаты после первых 100 деревьев.
3. Альтернативные подходы
Для решения данной проблемы стоит рассмотреть несколько альтернативных подходов:
-
Обмен метрик: Вы можете попробовать использовать более сложные метрики, такие как Huber Loss, которая является гладкой в одной области и линейной в другой. Это позволит модели осужденной на RMSE извлекать пользу от их преимуществ, в то время как вы по-прежнему контролируете влияние больших ошибок.
-
Комбинированные подходы: Можно рассмотреть возможность использования обучения на основе квадратных корней значений, как указано в ваших примерах. Вы можете взять корень из значений, обучить модель на этих трансформированных значениях, а затем возврату их к исходным результатам. Этот метод позволяет сохранять некоторые преимущества RMSE при минимизации общих ошибок.
-
Анализ предсказаний: Важно проанализировать, на каких конкретных экземплярах обе модели предсказывают неправильно и различия в этих предсказаниях. Это исследование может помочь вам понять, где именно одна модель обходит другую, и в конечном итоге дать вам представление о том, как можно улучшить оптимизацию.
Заключение
Оптимизация модели предсказания с использованием MAE может привести к неожиданным результатам, как вы и наблюдали. Однако понимание различий между метриками, их влияния на процесс оптимизации и рассмотрение альтернативных методов может помочь вам добиться более устойчивых и точных результатов. Рекомендации по использованию Huber Loss или комбинированных подходов могут оказаться жизнеспособными вариантами для преодоления ограничений, с которыми вы столкнулись при оптимизации MAE.