Квантование неопределенности в измерении площади с использованием Python и OpenCV

Я пытаюсь использовать OpenCV в сочетании с дешёвым USB-микроскопом для реального измерения площади образцов, которые мы готовим с помощью прокатки фольги, и которые в настоящее время измеряются с помощью штангенциркуля. Из-за неровных краёв некоторых образцов я хотел бы исследовать возможность использования анализа изображений, вместо того, чтобы делать предположения о том, что они круговые, прямоугольные и так далее. Кроме того, я хотел использовать миллиметровую сетку (на световом боксе, чтобы искать микроотверстия) за объектами, чтобы иметь возможность получить калибровку пиксель<->мм на лету. Это также значительно повышает контрастность, что облегчает установку порогов и избегание проблем с отражениями и т. д.

Это было успешно, но хотя площадь квадратов на сетке определяется точно, когда я изображаю объекты известного размера/площади (например, 1 цент США), я получаю значения, которые на 2-4% выше ожидаемых. Это можно было бы легко компенсировать изменением референсного значения до тех пор, пока калибровочный объект не будет измерен правильно, но я беспокоюсь, что это всего лишь временное решение проблемы, которую я делаю неправильно, возможно, с морфологическими преобразованиями / гауссовым размягчением, искажая края слишком сильно? Монета была проверкой калибровки, но не может находиться в кадре во время обычного использования, именно поэтому я хотел использовать сетку для калибровки с самого начала. Камера установлена вертикально над объектом и по центру, а попытка выполнить калибровку камеры, похоже, добавила больше сферической аберрации, чем улучшила ситуацию.

Это приводит к двум основным вопросам:

1. Что я делаю неправильно?
2. Возможно ли оценить неопределенность в площадях, рассчитанных через cv2.contourArea(contour)? Штангенциркули обычно позволяют нам достигать неопределенности менее 0,5% в измерениях площади, но количественная оценка неопределенности здесь была бы важна, хотя я не вижу информации об этом в документации…

Вот пример входного изображения с обычной монетой в 1 цент США, на бумаге с размером сетки 5 мм:

Градация серого:

Код для обнаружения квадратов сетки на заднем плане и возврата среднего значения калибровки пикселей<->мм:

def measureGridSize(img, show_plot=True):
    gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY) 
    grid_area_threshold = 100
    known_grid_width = 5 # мм

    outerBox = np.zeros(gray.shape, np.uint8)
    gray = cv2.GaussianBlur(gray,(3,3),0)

    outerBox = cv2.adaptiveThreshold(gray,255,cv2.ADAPTIVE_THRESH_MEAN_C, cv2.THRESH_BINARY_INV,3,2)

    kernel = np.array((
        [0, 1, 0],
        [1, 1, 1],
        [0, 1, 0]), dtype="uint8")

    # Разглаживаем края сеток, убираем артефакты бумаги
    outerBox = cv2.dilate(outerBox,kernel,iterations = 1)
    outerBox = cv2.morphologyEx(outerBox, cv2.MORPH_CLOSE, np.ones((2,2)))
    outerBox = cv2.morphologyEx(outerBox, cv2.MORPH_OPEN, np.ones((3,3)))
    outerBox = cv2.erode(outerBox,np.ones((3,4),np.uint8),iterations = 1)

    # Находим контуры
    contours, hierarchy  = cv2.findContours(outerBox, cv2.RETR_TREE, cv2.CHAIN_APPROX_SIMPLE)

    area_list = []
    contour_list = []

    for contour in contours:
        # находим моменты изображения
        M = cv2.moments(contour)

        try:
            cX = int(M["m10"] / M["m00"])
            cY = int(M["m01"] / M["m00"])
        except ZeroDivisionError:
            cX = 0
            cY = 0

        # если центр черный, значит контур ограничивает квадрат сетки
        if (outerBox[cY,cX] == 0) and (cY > 0) and (cX > 0):
            approxCurve = cv2.approxPolyDP(contour, 50, True)
            # если площадь прямоугольная
            if len(approxCurve)==4: 
                # получаем размеры сторон
                (x,y,w,h) = cv2.boundingRect(contour)
                delta = 0.2;
                area = area = cv2.contourArea(contour)

                cv2.drawContours(img, [contour], -1, (255,0,0), 3)  # изображаем все найденные контуры в синем
                cv2.drawContours(outerBox, [contour], -1, (255,0,0), 3)  # изображаем все найденные контуры в синем

                # Проверяем, выглядит ли контур как квадрат в пределах допуска 
                if (abs((w/h)-1) < delta) and (area > grid_area_threshold) and (abs((w*h/area)-1) < delta) :
                        if area > 0:
                            area_list.append(area)
                            contour_list.append(contour)

    for (area,contour) in zip(area_list,contour_list):
        cv2.drawContours(img, [contour], -1, (0,255,0), 3)  # изображаем квадратные контуры в зеленом

    # брать медиану или среднее для масштабирования сетки?
    # Убираем крайние случаи, чтобы отбросить шум
    area_list.sort()
    if len(area_list) < 2:
        median = np.mean(area_list)
    elif len(area_list) < 3:
        median = np.mean(area_list[1:-1])
    else:
        median = np.mean(area_list[2:-2])
    pixels_per_mm = 0

    # считаем сторону квадрата, которая равна количеству пикселей на миллиметр
    if np.size(median) == 1:
        pixels_per_mm = np.sqrt(median) / known_grid_width

    # Аннотируем площадь на каждом обнаруженном квадрате сетки для сравнения
    for contour in contour_list:
        area = cv2.contourArea(contour)
        if area > grid_area_threshold:

            x, y, w, h = cv2.boundingRect(contour) 
            cv2.putText(img, '{0:.2f}'.format(area/(pixels_per_mm*pixels_per_mm)), (x, y+20), cv2.FONT_HERSHEY_SIMPLEX, 0.75, (0, 0, 255), 2) 

    return pixels_per_mm    

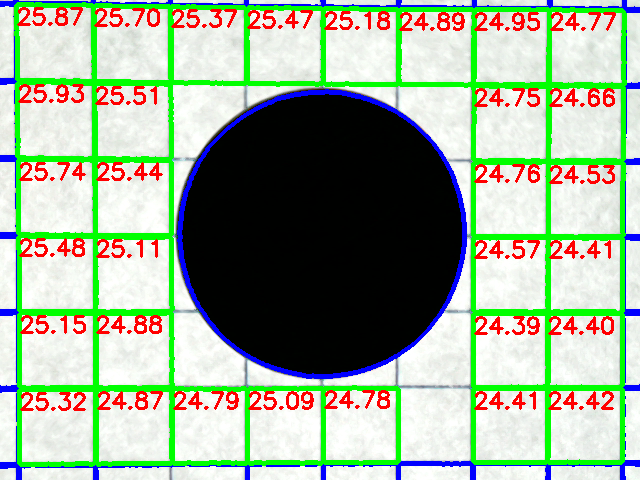
с выводом:

Код, который берет калибровку пикселей на миллиметр и измеряет площадь объектов при установленном пороге:

def measureArea(img, pixels_per_mm):
    area_threshold = 100  # Отбрасываем мелкие детали

    # Преобразуем в градации серого 
    gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY) 

    #
    # Обнаружение порогов
    #

    blur = cv2.GaussianBlur(gray, (5, 5), 0)
    ret,th1 = cv2.threshold(gray,70,255,cv2.THRESH_BINARY)

    contours,hierarchy = cv2.findContours(th1, 1, 2)
    for contour in contours:
        area = cv2.contourArea(contour)
        # Аннотируем площадь объекта на изображении
        if area > area_threshold:

            x, y, w, h = cv2.boundingRect(contour) 
            cv2.putText(img, '{0:.2f} см²'.format(area/(pixels_per_mm*pixels_per_mm*100)), (x, y), cv2.FONT_HERSHEY_SIMPLEX, 1, (0, 0, 255), 2) 

            cv2.drawContours(img, [contour], -1, (0,255,0), 1)  # изображаем квадратные контуры в зеленом

с выводом:

И наконец, код, который просто перебирает поток камеры и вызывает два вышеуказанных метода, и делает скользящее среднее пикселей на миллиметр, чтобы сгладить выходные значения площади (чтобы избежать дрожания значений в реальном времени):

def acquireFromCamera(show_calibration=False):
    # Открываем камеру по умолчанию (по умолчанию было 0)
    cam = cv2.VideoCapture(0)

    pixel_scale_list = []

    # Цикл по кадрам входного потока камеры
    while True:
        # Переключено с ввода камеры на imread для публикации на stackoverflow
        # 
        # ret, frame = cam.read()
        frame = cv2.imread('original_image.png')
        frame_copy = frame.copy()

        pixels_per_mm = measureGridSize(frame)

        # Получаем скользящее среднее пиксельного масштаба для сглаживания выходных площадей
        if not np.isnan(pixels_per_mm):
            pixel_scale_list.append(pixels_per_mm)
        avg_pixel_scale = np.convolve(pixel_scale_list, np.ones(len(pixel_scale_list))/len(pixel_scale_list), mode="valid")

        print(avg_pixel_scale)
        measureArea(frame_copy, avg_pixel_scale[0])
        if show_calibration:
            cv2.imshow('Обнаружение площади', frame_copy)

        # Отображаем захваченный кадр
        cv2.imshow('Камера (нажмите q для выхода)', frame)

        if cv2.waitKey(1) == ord('q'):
            break

    # Освобождаем захват и объекты записи
    cam.release()
    cv2.destroyAllWindows()

acquireFromCamera(True)

Использование known_grid_width = 5 # мм для бумаги с размером сетки 5 мм генерирует точные измерения площадей квадратов сетки (в среднем 24.94398288816283 мм²), но переоценивает ожидаемую площадь монеты в 2.853 см² примерно на 3%. Уменьшение known_grid_width для правильной площади монеты делает площади квадратов сетки около 23.8 мм², что является серьёзной недооценкой, а измерения штангенциркуля сетки бумаги выглядят последовательными с 5 мм. Я не думаю, что это проблема с порогами для measureArea(), а использование среднего против медианы для получения представительного значения пикселей на мм в каждой итерации цикла также кажется довольно не чувствительным. Если это проблема с морфологическими преобразованиями в обнаружении сетки, выбор ядра был ОЧЕНЬ чувствителен к тому, сколько квадратов сетки вообще было обнаружено. Не имея временного решения с использованием площади монеты вместо known_grid_width (и тем самым опровергая всю цель бумаги), как я могу согласовать результаты площадей сетки с монетой?

Буду признателен за любую помощь, которую вы можете предоставить, особенно в оценке неопределенности в соответствиях площади! Спасибо!!