Граничная линия решения в задаче классификации

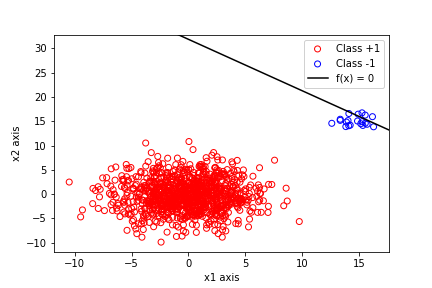
У меня есть 1000 данных из двувариантного нормального распределения $\mathcal{N}$ со средним $(0,0)$ и дисперсией $\sigma_1^2=\sigma_2^2=10$, при этом ковариация равна $0$. Также есть еще 20 точек из другого двувариантного нормального распределения со средним $(15,15)$, дисперсией $\sigma_1^2=\sigma_2^2=1$ и ковариацией $0$. Я использовал метод наименьших квадратов для расчета параметров границы решения $\theta_0 + \theta_1 x_1 + \theta_2 x_2=0$, то есть $$\theta = (X^T X)^{-1}(X^Ty)$$, где $y$ – это столбцовая матрица с метками $+1$ для точек из первого класса и $-1$ для точек из второго. Результирующий график выглядит следующим образом:

Явно видно, что граница решения оказалась неверной, так как она проходит прямо через класс $-1$, и поэтому не будет правильно классифицировать будущие точки, которые могут принадлежать тому же распределению. Теперь возникает вопрос, почему это происходит. Я понимаю, что главная проблема здесь – это несоответствие данных, так как есть $1000$ точек из одного класса и только $20$ из другого. Это интуитивно имеет смысл.

Что я хочу, чтобы кто-то мне объяснил, если это возможно, так это как эта проблема несоответствия встраивается в процесс минимизации функции стоимости наименьших квадратов $$J(\theta)=\sum_{n=1}^{200}(y_n-\theta^T x_n)^2$$

Почему тот факт, что есть только $20$ точек из второго класса, приводит к “провалу” задачи минимизации $\frac{\partial J(\theta)}{\partial \theta}=0$? Как недостаточное количество этих точек вызывает то, что линия проходит прямо через них? Если есть какой-то математический способ показать это, было бы неплохо, так как у меня уже есть интуиция.

Для этих данных порог, расположенный на оси x1, прекрасно разделит два распределения. Вы можете подогнать решение до расчета единственного параметра границы решения.

Я утверждаю, что это особенность, а не ошибка.

Говоря о классификации, не зная значений $x_1$ или $x_2$, гораздо вероятнее, что ваша точка принадлежит $+1$ чем $-1$. Следовательно, вам не нужно просто достаточно доказательств того, что точка – это $-1$. Вам нужны убедительные доказательства.

Красная группа $+1$, грубо говоря, существует в квадрате $[-10,10]\times[-10,10]$. Ближайшая синяя точка $-1$ находится примерно в $(12,15)$, что не так уж далеко от зоны $+1$. Граница решения говорит вам, что $(12,15)$ не находится достаточно далеко от зоны $+1$, чтобы преодолеть высокую “априорную” вероятность принадлежности к классу $+1$. Чтобы находиться достаточно далеко от зоны $+1$, чтобы не быть классифицированным как $+1$, вам нужно быть выше примерно $(15,17)$.

Если вы сымитируете $100$, затем $200$, а затем $500$, а затем $1000$ синих $-1$ точек в дополнение к тем же $1000$ красным $+1$ точкам, вы увидите, как граница решения сдвигается к тому месту, где вы ожидаете, что она будет между двумя группами.

Вы можете использовать эту идею “априорной” (и “апостериорной”) вероятности больше, если используете логистическую регрессию для прогнозирования вероятностей принадлежности к классам. Хотя это может потребовать нового вопроса, это может быть более связано с “математическим” объяснением, которое вам нужно.

Прежде всего, ваша линейная модель вероятности значительно отличается от логистической регрессии. Последняя не имела бы проблем с разделением этих классов; коэффициенты уедут к бесконечности, пытаясь вытолкнуть предсказанные логарифмические шансы к $\pm\infty$, но в любом месте, где вы остановите процесс, у вас будет идеальное разделение.

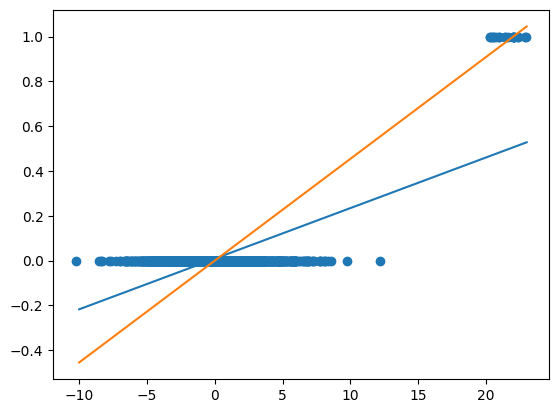
Таким образом, это действительно больше проблема регрессии, чем классификации. И две размерности на самом деле отвлекают от сути, поэтому вот версия с одной размерностью:

Синяя линия – это подогнанная линейная регрессия, оранжевая – то, что, как мне кажется, вы считаете более естественным. Проблема заключается в довольно большом количестве точек около $x=\pm5$ (например, конечно, принимая во внимание все точки): согласно оранжевой модели, квадратная ошибка в этом месте значительно больше, и поскольку таких точек значительно больше, чем точек с $y=1$, общая потеря $J$ получает преимущество с синей линией.

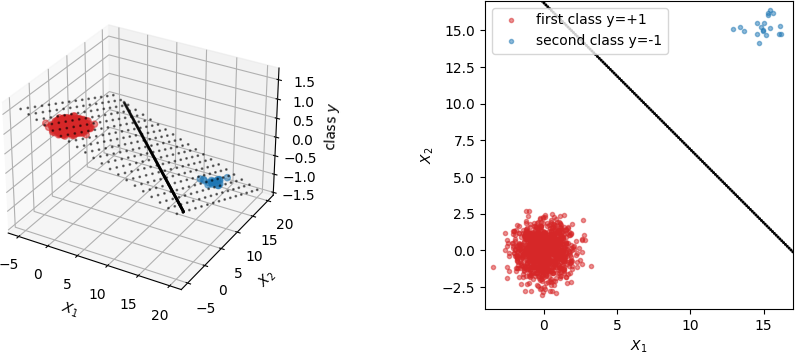
Прежде всего, график в вопросе не выглядит правильным. Вот что я получу, если выполню те же расчеты:

Там, слева небольшие маркеры показывают плоскость в “3D”, которая является результатом замкнутого решения, данного @thenac (что на самом деле является решением проблемы регрессии). Линия, показанная на обоих графиках, – это граница решения, т.е. место, где плоскость имеет “класс y=0”. Чем меньше данных для второго класса, тем более горизонтальной становится плоскость решения (поскольку красные маркеры имеют больший вес по сравнению с синими) и тем дальше граница решения уходит от класса большинства. Это также связано с минимизацией наименьших квадратов с заданной функцией стоимости.

Использовать наименьшие квадраты для классификации определенно не лучший выбор, так как это не надежно при добавлении новых данных, но это не был вопрос.

(в конце концов, также можно математически записать, как $J$ и $\partial J/\partial \theta$ выглядят для упрощенной ситуации, когда все точки данных точно расположены в одной или другой точке. Тогда это действительно всего лишь взвешивание двух терминов, появляющихся в $J(\theta)$.)