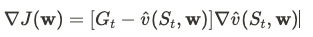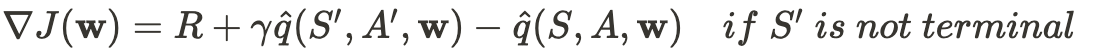Вопрос или проблема
Я изучал теорию и практику RL, и одна часть, которую мне трудно понять, — это связь между практической функцией loss и теоретической целью/градиентом цели. Как мы можем вывести одно из другого? Возможно, это будет легче понять на примерах:
Reinforce с базовой линией:
Теоретический градиент целевой функции критика
Практическая функция потерь (псевдокод), которую я встречал:
critic_loss = 0.5 * (returns - v_hat(states))**2
Сарса с полу-градиентом:
Теоретический градиент целевой функции
Практическая функция потерь (псевдокод), которую я встречал:
loss = (r + gamma * qvalue(s_next,a_next) - qvalue(s,a)) ** 2
Откуда это берется? Является ли это отрицательным обратным ∇J(w)? Если да, может кто-то показать, как это делается? Я нахожу ресурсы только по этой теме для w фиксированных размеров.
Возможно, я совершенно ошибаюсь и не понимаю каких-то основ. Если это так, буду искренне благодарен, если вы направите меня на соответствующую (вводную) литературу.
Псевдокод соответствует следующему: (для первого примера)
$$ J(w)=\frac{1}{2}(G_t-\hat{v}(s_t, w))^2 $$
Вы можете получить первое выражение, просто явно вычислив градиент.
$$ \nabla_w J(w)=-(G_t-\hat{v}(s_t, w))\nabla_w \hat{v}(s_t, w) $$
Для второго примера я не уверен в вашем источнике, но я думаю, что это должно быть так (см. стр. 244 в Sutton-Barto)
$$R+\gamma \hat{q}(s’,a’,w)-\hat{q}(s,a,w))\nabla_w\hat{q}(s,a,w). $$
Теперь действительно, это не градиент
$$ J(w)=\frac{1}{2}(R +\gamma \hat{q}(s’,a’,w)-\hat{q}(s,a,w)))^2$$
Наверное, в коде должно быть больше контекста, и с высокой вероятностью есть какой-то stop gradient (в TensorFlow) или detach (в PyTorch), чтобы указать, что если мы берем градиент этой функции потерь, это действительно соответствует нужному обновлению (то есть мы пренебрегаем тем, что $\hat{q}(s’,a’,w)$ зависит от $w$ при вычислении градиента). Этот трюк используется для того, чтобы мы могли использовать вычислительно эффективную обратную передачу ошибки.
Ответ или решение
Вопрос о том, как из теоретической градиентной функции цели получается практическая функция потерь, нередко вызывает путаницу, особенно в контексте обучения с подкреплением (RL). Давайте разберемся в этом вопросе на примере двух подходов: Reinforce с базисом и Semi-gradient SARSA.
Определение функции потерь из градиентной цели
Reinforce с базисом
Теоретическая цель:
На данном этапе важно понимать, что цель заключается в минимизации отклонения между ожидаемым вознаграждением и оценкой ценности состояния. Теоретическая цель представлена как градиент:
[ \nabla_w J(w) = -(G_t – \hat{v}(s_t, w))\nabla_w \hat{v}(s_t, w) ]
Практическая функция потерь (псевдокод):
critic_loss = 0.5 * (returns - v_hat(states))**2Пояснение:
Формула потерь, используемая в коде, по сути представляет собой квадратичную функцию от разности между эмпирическим возвратом и предполагаемой ценностью состояния (v). Причина, по которой градиент целевой функции выглядит иначе, заключается в том, что формула в псевдокоде уже подразумевает использование цепного правила для обновления параметров (w). Здесь мы вычисляем производную по параметрам и используем скорректированное значение для обновления.
Semi-gradient SARSA
Теоретическая цель:
Обновление по Semi-gradient SARSA выглядит следующим образом:
[ R + \gamma \hat{q}(s’, a’, w) – \hat{q}(s, a, w) ]
Практическая функция потерь (псевдокод):
loss = (r + gamma * qvalue(s_next, a_next) - qvalue(s, a)) ** 2Пояснение:
В этом случае мы работаем с разницей между ожидаемой ценностью действия и текущей оценкой (q)-функции. Потери представляют собой квадратичную разницу, которая минимизируется с использованием градиентного спуска. Определяющим фактором здесь является то, что градиент не берется в отношении следующего состояния, что объясняет использование оператора остановки градиента («stop gradient») в библиотеке синтаксиса (например, TensorFlow или PyTorch).
Заключение
Связь между градиентной функцией цели и функцией потерь часто оказывает влияние на вычислительную эффективность алгоритма. Важно понимать, как используются цепное правило и механизмы остановки градиента для оптимизации вычислений. Для более детального изучения вы можете обратиться к классическому руководству Ричарда Саттона и Эндрю Барто "Reinforcement Learning: An Introduction". Оптимизация функции потерь является ключевым этапом на пути к повышению эффективности модели.
Это чтение поможет вам более четко понять динамику преобразования теоретических концепций в практические реализации. Помните, что глубокое понимание теоретических основ позволит эффективно применять их на практике.