Вопрос или проблема
Я думал, что и PReLU, и Leaky ReLU это:
$$f(x) = \max(x, \alpha x) \qquad \text{ где } \alpha \in (0, 1)$$
Keras, однако, имеет обе функции в документации.
Leaky ReLU
return K.relu(inputs, alpha=self.alpha)
Следовательно (см. код relu):
$$f_1(x) = \max(0, x) – \alpha \max(0, -x)$$
PReLU
def call(self, inputs, mask=None):
pos = K.relu(inputs)
if K.backend() == 'theano':
neg = (K.pattern_broadcast(self.alpha, self.param_broadcast) *
(inputs - K.abs(inputs)) * 0.5)
else:
neg = -self.alpha * K.relu(-inputs)
return pos + neg
Следовательно:
$$f_2(x) = \max(0, x) – \alpha \max(0, -x)$$
Вопрос
Я что-то не так понял? Разве $f_1$ и $f_2$ не эквивалентны $f$ (при условии $\alpha \in (0, 1)$?)
Leaky ReLUs позволяют небольшому ненулевому градиенту, когда узел не активен:
$$f(x) = \begin{cases}
x & \text{если $x>0$}\\
\mathbf{0.01}x & \text{в противном случае}
\end{cases} $$
Параметрические ReLUs развивают эту идею дальше, делая коэффициент утечки ($0.01$ выше) параметром, который обучается вместе с другими параметрами нейронной сети:
$$f(x) = \begin{cases}
x & \text{если $x>0$}\\
\alpha x & \text{в противном случае}
\end{cases} $$
Где $\alpha$ — это обучаемый параметр, который обучается методом градиентного спуска, подобно другим параметрам нейронной сети, таким как веса и смещения. Источник
Довольно старый вопрос; но я добавлю еще одну деталь, на случай если кто-то еще окажется здесь.
Мотивация за PReLU заключалась в том, чтобы преодолеть недостатки ReLU (проблема умирающего ReLU) и LeakyReLU (неконсистентные предсказания для отрицательных входных значений).
Поэтому авторы статьи о PReLU думали, почему бы не позволить a в ax для x<0 (в LeakyReLU) обучаться!!
И вот в чем подвох: если все каналы делят один и тот же a, который обучается, это называется PReLU с общим каналом. Но если каждый канал обучает свой собственный a, это называется PReLU с учетом каналов.
Так что если ReLU или LeakyReLU оказались лучше для этой проблемы? Это зависит от модели:
- если a обучается как 0 –> PReLU становится ReLU
- если a обучается как маленькое число –> PReLU становится LeakyReLU
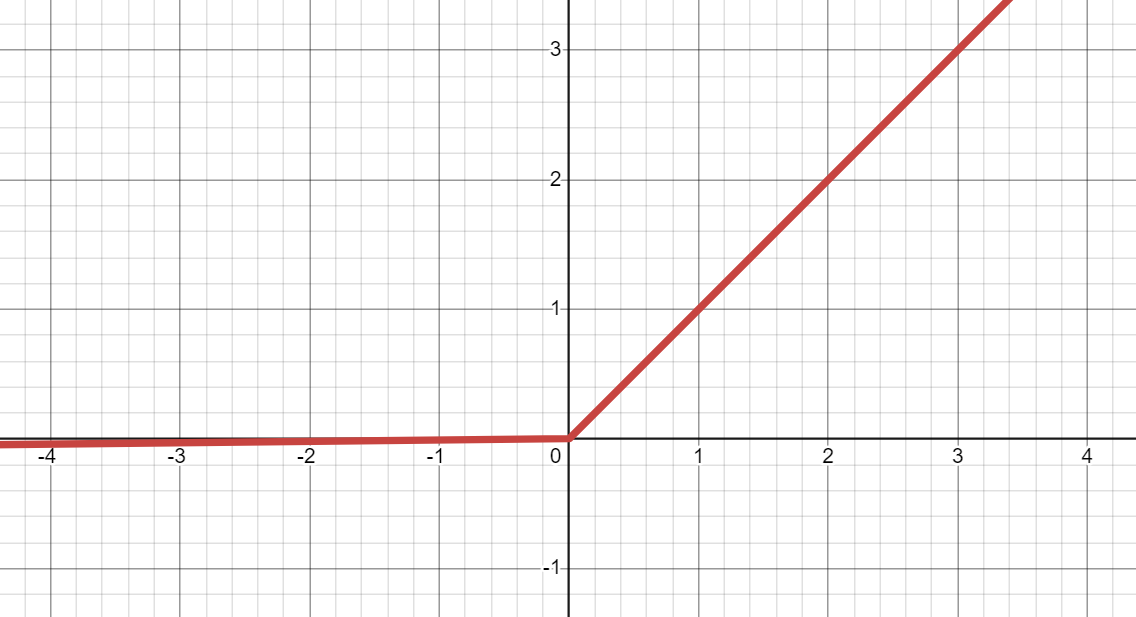
Leaky ReLU (Leaky Rectified Linear Unit):
- является улучшенной версией ReLU, способной смягчать Проблему умирающего ReLU.
- может преобразовать входное значение (
x) в выходное значение междуaxиx.
*Записки:- Если
x< 0, тоax, а если 0 <=x, тоx. aпо умолчанию равен 0.01.
- Если
- также называется LReLU.
- является LeakyReLU() в PyTorch.
- используется в:
- GAN.
- плюсы:
- Усмягчает Проблему убывающего градиента.
- Усмягчает Проблему умирающего ReLU. *0 все равно выдается для входного значения 0, поэтому Проблема умирающего ReLU полностью не устранена.
- минусы:
- Не является дифференцируемым в
x=0.
- Не является дифференцируемым в
- график Leaky ReLU в Desmos:
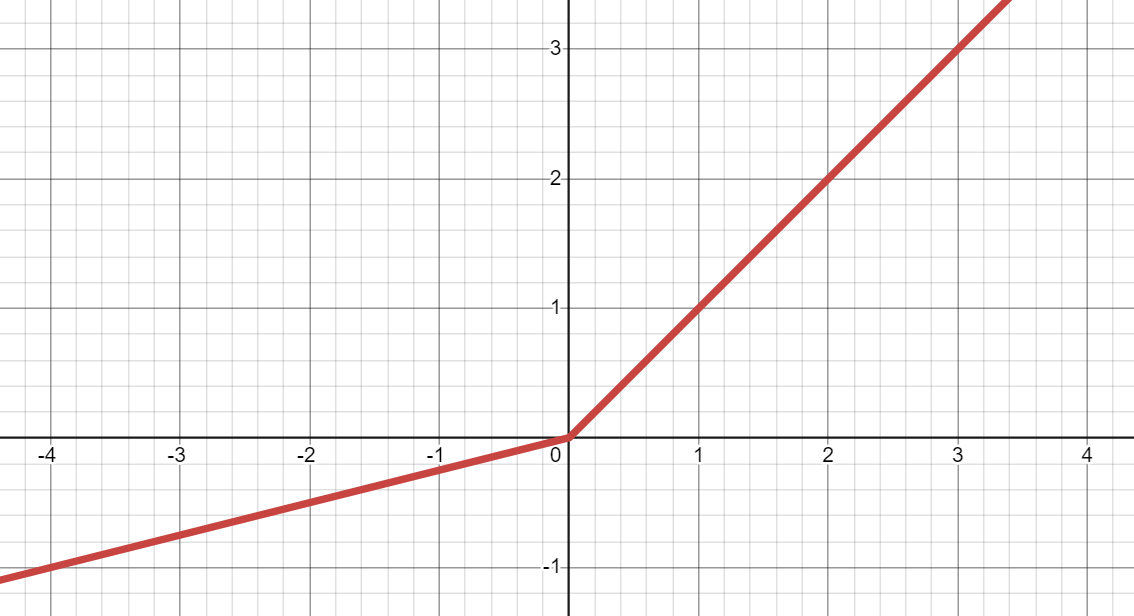
PReLU (Параметрическая исправленная линейная единица):
- является улучшенной версией Leaky ReLU, имеющей 0 или более обучаемых параметров, которые меняются (настраиваются) в процессе обучения для улучшения точности и сходимости модели.
- может преобразовать входное значение (
x) в выходное значение междуaxиx:
*Записки:- Если
x< 0, тоax, а если 0 <=x, тоx. aпо умолчанию равен 0.25. *aявляется начальным значением для 0 или более обучаемых параметров.
- Если
- является PReLU() в PyTorch.
- используется в:
- SRGAN (Сетевое противодействие для повышения разрешения). *SRGAN — это тип GAN (Сетевое противодействие генераторов).
- плюсы:
- Усмягчает Проблему убывающего градиента.
- Усмягчает Проблему умирающего ReLU. *0 все равно выдается для входного значения 0, поэтому Проблема умирающего ReLU полностью не устранена.
- минусы:
- Не является дифференцируемым в
x = 0. *Градиент для ступенчатой функции не существует приx = 0во время Обратного распространения, что не дает возможности вычислить и получить градиент.
- Не является дифференцируемым в
- график PReLU в Desmos:
Ответ или решение
Leaky ReLU и PReLU: Подробное Сравнение
В мире глубокого обучения активационные функции играют важнейшую роль в обучении нейронных сетей. Среди них Leaky ReLU (Ликирующая Ректифицированная Линейная Единица) и PReLU (Параметрическая Ректифицированная Линейная Единица) являются двумя популярными вариантами, которые часто используются для решения проблем с убывающими градиентами и «умирающими» нейронами. Хотя они имеют схожую основу, ключевые различия между ними крайне важны для выбора правильной функции активации для конкретной задачи.
Leaky ReLU
Leaky ReLU представляет собой усовершенствованную версию стандартной функции ReLU. Основная функция Leaky ReLU формулируется следующим образом:
$$
f(x) = \begin{cases}
x & \text{если } x > 0 \
\alpha x & \text{иначе}
\end{cases}
$$
где $\alpha$ – это небольшой коэффициент (обычно 0.01), который позволяет функции принимать некоторый отрицательный градиент, когда входное значение $x$ меньше или равно нулю. Это помогает избежать проблемы «умирающего ReLU», когда нейрон перестает обучаться, потому что его выход всегда равен нулю.
Преимущества Leaky ReLU:
- Смягчение проблемы убывающего градиента: Наличие небольшого отрицательного градиента позволяет поддерживать обучение для некоторой части нейронов.
- Простота реализации: Легкая интеграция в любую нейросеть без дополнительных параметров.
Недостатки Leaky ReLU:
- Ненадежность: Значение $\alpha$ фиксировано и не в состоянии адаптироваться в зависимости от задачи или данных.
PReLU
PReLU является ещё шагом вперёд от Leaky ReLU. Она вводит learnable параметр $\alpha$, который модели позволяет адаптировать значение для каждой нейронной единицы или канала. Основная функция PReLU может быть записана как:
$$
f(x) = \begin{cases}
x & \text{если } x > 0 \
\alpha x & \text{иначе}
\end{cases}
$$
где $\alpha$ обучается во время тренировки сети, позволяя сети находить оптимальное значение для каждого случая.
Преимущества PReLU:
- Адаптивность: Параметр $\alpha$ подстраивается под данные, что позволяет функции лучше приспосабливаться к конкретной задаче и уменьшает случайность выводов для отрицательных значений.
- Улучшение прогноза: Выбор наилучшего значения $\alpha$ для каждой активации может улучшить как сходимость сети, так и accuracy модели.
Недостатки PReLU:
- Сложность: Увеличивает количество параметров модели, что может привести к большему времени обучения.
- Ненадежность на значениях 0: FПохожие функции, включая и Leaky ReLU, PReLU также оказывается не дифференцируемой в точке $x = 0$.
Выводы
Обе функции попытались решить проблему «умирающего ReLU», но делают это по-разному. Leaky ReLU использует фиксированное значение для градиента на отрицательных входах, тогда как PReLU обеспечивает возможность обучения этого значения, что делает её более гибкой и адаптивной для разнообразных задач.
- Leaky ReLU: Подходит для случаев, когда решающие параметры модели должны оставаться простыми, когда отсутствует необходимость в большой гибкости.
- PReLU: Рекомендуем для сложных сетей, где требуется высокая точность, и время на обучение не является критическим фактором.
В конечном счете, выбор между Leaky ReLU и PReLU должен зависеть от специфики задачи, доступных вычислительных ресурсов и желаемой производительности модели.