Вопрос или проблема
Я пытаюсь построить многовариантную линейную регрессию, и основная цель заключается в том, чтобы понять, как различные характеристики влияют на отклик, изучая коэффициенты и их доверительные интервалы.
По этой причине я выбрал многовариантную линейную регрессию, потому что коэффициенты интуитивно понятны для интерпретации, и по стандартной ошибке и степени свободы я могу получить 95% доверительный интервал коэффициентов. Таким образом, я могу определить, каков эффект увеличения на единицу предиктора на результат. Я мог бы использовать более сложные модели, такие как модели на основе деревьев, но даже если я могу получить важность переменных, не так просто количественно оценить коэффициент каждой переменной.
Моя проблема, однако, в том, что данные являются временными рядами и, следовательно, показывают автокорреляцию. Я знаю, что использование регрессии с ошибками ARIMA может справиться с проблемой автокорреляции, но мне оказалось трудно интерпретировать коэффициенты, особенно когда d не равно нулю в ARIMA(p, d, q). Приложенное изображение, например, является диагностикой модели для одной из моделей, которые у меня есть (мне нужно построить их тысячи).
Как я могу справиться с проблемой автокорреляции и все же получить коэффициенты, которые легко интерпретируемы, как в многовариантной линейной регрессии? Мои остатки не распределены нормально, и я планирую использовать преобразование Бокса-Кокса, чтобы увидеть, может ли это решить проблему. Но я не уверен, что использовать для проблемы автокорреляции.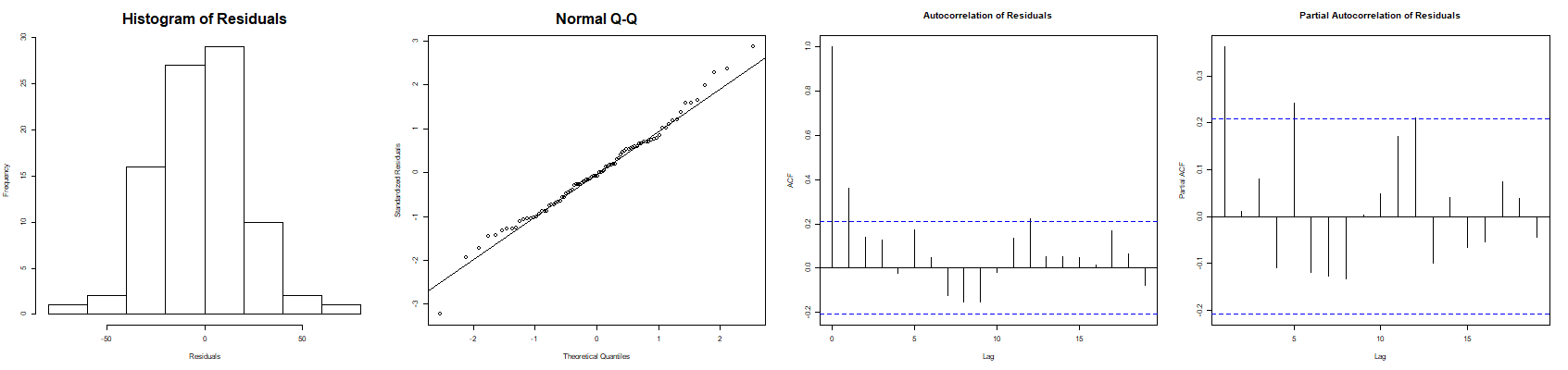
Чтобы справиться с автокорреляцией, вы должны попытаться “вычесть ее” из ряда. Другими словами, используя дифференцирование, десезонализацию и преобразования, вы должны попытаться вычесть влияние времени на данные временного ряда. Как только вы получите распределение, похожее на белый шум, вы можете провести свою регрессию.
Вы можете сделать это с помощью модели ARIMA, просто добавьте все компоненты AR(), I() и MA() в уравнение регрессии, а затем проигнорируйте их, когда оцениваете влияние других коэффициентов.
Ответ или решение
Создание многомерной линейной регрессии для анализа влияния предикторов на отклик может быть сложной задачей, особенно когда данные представлены в виде временных рядов и демонстрируют автокорреляцию. В этой статье я детально рассмотрю возможные подходы к решению данной задачи, основываясь на вашем описании проблемы.
Понимание влияния предикторов при помощи коэффициентов
Преимуществом многомерной линейной регрессии является интуитивная интерпретация коэффициентов. Коэффициенты указывают на изменение ожидаемого значения отклика при изменении предиктора на единицу, при прочих равных условиях. Однако при наличии автокорреляции сама применимость этих коэффициентов может быть поставлена под сомнение.
Проблема с автокорреляцией
Временные ряды часто содержат автокорреляцию, и ее игнорирование может привести к смещению результатов. Один из возможных методов решения этой проблемы — использование регрессии с ошибками типа ARIMA, однако у вас возникли трудности с интерпретацией коэффициентов, особенно когда параметр дифференцирования d отличается от нуля.
Возможные решения проблемы автокорреляции
- Предварительная обработка данных: Рассмотрите возможность разложения временного ряда на тренды и сезонные компоненты. Использование дифференцирования и десезонирования может помочь достичь стационарности, что облегчит последующий анализ.
- Преобразование данных: Применение преобразования Бокса-Кокса может помочь в нормализации распределения остатков, хотя и не всегда убирает автокорреляцию.
- Построение модели ARIMA и выделение автокорреляции: Как вы уже упомянули, интересным подходом является использование компонентов AR (авторегрессии), I (интеграции) и MA (скользящего среднего) в комбинации с регрессией. Эти компоненты “вычитают” автокорреляцию, оставляя вам интерпретировать коэффициенты регрессии для других предикторов.
- Проверка на стационарность: Проверьте, достигнут ли стационарный вид данных посредством тестов (например, теста Дики-Фуллера).
Рекомендации
Если ваша цель заключается в интерпретации и выделении вклада различных предикторов, учтите следующие рекомендации:
- Изучите методы предварительной обработки данных для избавления от автокорреляции.
- Используйте диаграммы коррелограмм для визуальной оценки автокорреляции и подбора правильных параметров ARIMA модели.
- Протестируйте различные модели и их производные, сохраняя фокус на интерпретации коэффициентов.
На основании вашего описания, основное внимание следует уделить предварительной корректировке временных данных. Это облегчит процесс регрессионного анализа и интерпретации, сохранив при этом информативность и достоверность моделей.