Оценка сходств и различий групп после PCA

Цель состоит в оценке сходства и различия между 6 известными группами.

Исходные данные начинались с 6 известных групп и 2700+ переменных, все на шкале от 0 до 100.

Я выполнил PCA, чтобы уменьшить более чем 2700 переменных до 5 главных компонентов, используя функцию dudi.pca из пакета ade4 в R. Вот собственные значения для компонентов:

      eigenvalue variance.percent cumulative.variance.percent
Dim.1   998.3274        36.635867                    36.63587
Dim.2   670.1278        24.591848                    61.22771
Dim.3   482.2372        17.696776                    78.92449
Dim.4   352.2806        12.927728                    91.85222
Dim.5   222.0270         8.147781                   100.00000

Теперь я хотел бы оценить расстояния между 6 известными группами. Это делается так же просто, как создание матрицы расстояний, используя координаты каждой группы для каждого из главных компонентов? Если да, то я склоняюсь к использованию манхэттенского расстояния, чтобы получить абсолютное расстояние.

Вот координаты каждой группы:

           Dim.1       Dim.2       Dim.3        Dim.4        Dim.5
Group 1    69.019038    7.940190    0.4985599  - 6.847178     0.3964117
Group 2   -16.302322  -25.965373  -29.3084201  -23.013430     9.9183010
Group 3   -26.313850   50.159662    6.9486408  -10.713924     5.2883152
Group 4   -12.800767  -26.211432   39.5067264  - 8.775551   - 8.8840592
Group 5   - 9.228404    2.648632  -20.4297314   16.685426   -26.8559444
Group 6   - 4.373694   -8.571679    2.7842244   32.664657    20.1369757

Если нет, то каков будет подходящий способ оценить индивидуальное сходство/различие после PCA?

Что означает расстояние между группами для вашей задачи? Ответ на этот вопрос поможет вам выбрать метрику расстояния.

Предположим, вы выбрали, например, евклидово расстояние, простым способом нахождении расстояния между группами будет сначала вычислить центр групп, т.е. среднее местоположение каждой группы путем усреднения местоположений каждой группы. Вы можете сделать это, просто усреднив все 5×1 векторы, принадлежащие группе, и повторить для каждой группы. Затем вычислите евклидово расстояние между получившимися 6 центрами, что даст вам матрицу расстояний 6×6.

Чтобы измерить, какие характеристики являются “движущими силами различия между группами”, вам нужно будет сформулировать это как задачу классификации. В рамках этого подхода вы можете использовать важность переменных (и потенциально значения коэффициентов, в зависимости от модели), чтобы провести вывод о движущих силах, т.е. для их идентификации и ранжирования.

Применение PCA в качестве предварительного шага значительно усложнит идентификацию переменных, которые являются двигателями для конкретных классов. PCA безразличен к присвоению классов: вы можете использовать компоненты и загрузки собственных векторов PCA для интерпретации того, какие переменные ответственны за основную часть вариации в ваших данных, но это не то, что вам нужно. Представьте, если ваши классы были бы длинными эллипсоидными кластерами, каждый с точно такой же матрицей ковариации, но с разным центром (т.е. эллипсы “параллельны”): компоненты, заданные PCA, в основном были бы подвержены влиянию формы эллипсоида (т.е. общей матрице ковариации), а не различиям между группами. Если вас интересует понимание движущих сил различий между группами, я настоятельно рекомендую отказаться от шага PCA.

У меня все еще нет четкого представления о том, что именно вы надеетесь получить из “какие группы наиболее похожи”, но я подозреваю, что мера “ближайшего соседства”, заданная случайными лесами, удовлетворит вашу потребность здесь. Эта мера фактически находится между наблюдениями, но вы можете взять средние значения, чтобы получить ожидаемое соседство между группами. Преимущество использования случайных лесов здесь в том, что у них есть встроенные меры важности переменных, и вы можете даже проанализировать их, чтобы понять движущие силы отдельных наблюдений.

Вот небольшая демонстрация, показывающая, как использовать модель случайного леса для выявления движущих сил через важность переменных и измерения сходства групп через среднее межнаблюдательное соседство:

Сначала подготовьте данные и обучите модель

library(randomForest)
data(iris)
set.seed(123)

unq_classes <- unique(iris$Species)
n_classes   <- length(unq_classes)

iris.rf <- randomForest(Species ~ ., data=iris, 
                        importance=TRUE,
                        proximity=TRUE)

Важности переменных, пересчитанные в [0,1], где “1” указывает на наиболее важную переменную:

var_imp <- importance(iris.rf)[,1:(n_classes+1)]
var_imp <- apply(var_imp, 2, function(m) m/max(m))

Вот результат (последний столбец — это маргинализированная важность):

                    setosa versicolor virginica MeanDecreaseAccuracy
Sepal.Length 0.2645863  0.2403256 0.2503047            0.3336813
Sepal.Width  0.1927240  0.0314708 0.1716495            0.1564093
Petal.Length 0.9525359  0.9589636 0.9356667            0.9549433
Petal.Width  1.0000000  1.0000000 1.0000000            1.0000000

А наши средние соседства, снова пересчитанные в [0,1], где 1 указывает на наиболее похожую пару групп:

prx <- iris.rf$proximity
mean_prx <- matrix(NA, n_classes, n_classes)
for (i in 1:(n_classes-1)){
  for (j in (i+1):n_classes){
    cls_i <- iris$Species == unq_classes[i]
    cls_j <- iris$Species == unq_classes[j]
    mean_prx[j,i] <- mean(prx[cls_i, cls_j])
  }
}

mean_prx <- mean_prx/max(mean_prx, na.rm=TRUE)
rownames(mean_prx) <- unq_classes
colnames(mean_prx) <- unq_classes

Что дает нам:

                 setosa versicolor virginica
setosa               NA         NA        NA
versicolor 0.0267520374         NA        NA
virginica  0.0007778552          1        NA

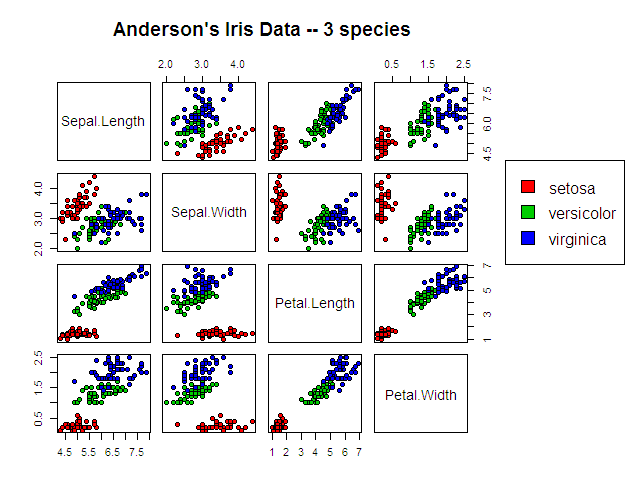
Вот как выглядят данные, чтобы поставить эти результаты в контекст: