Вопрос или проблема
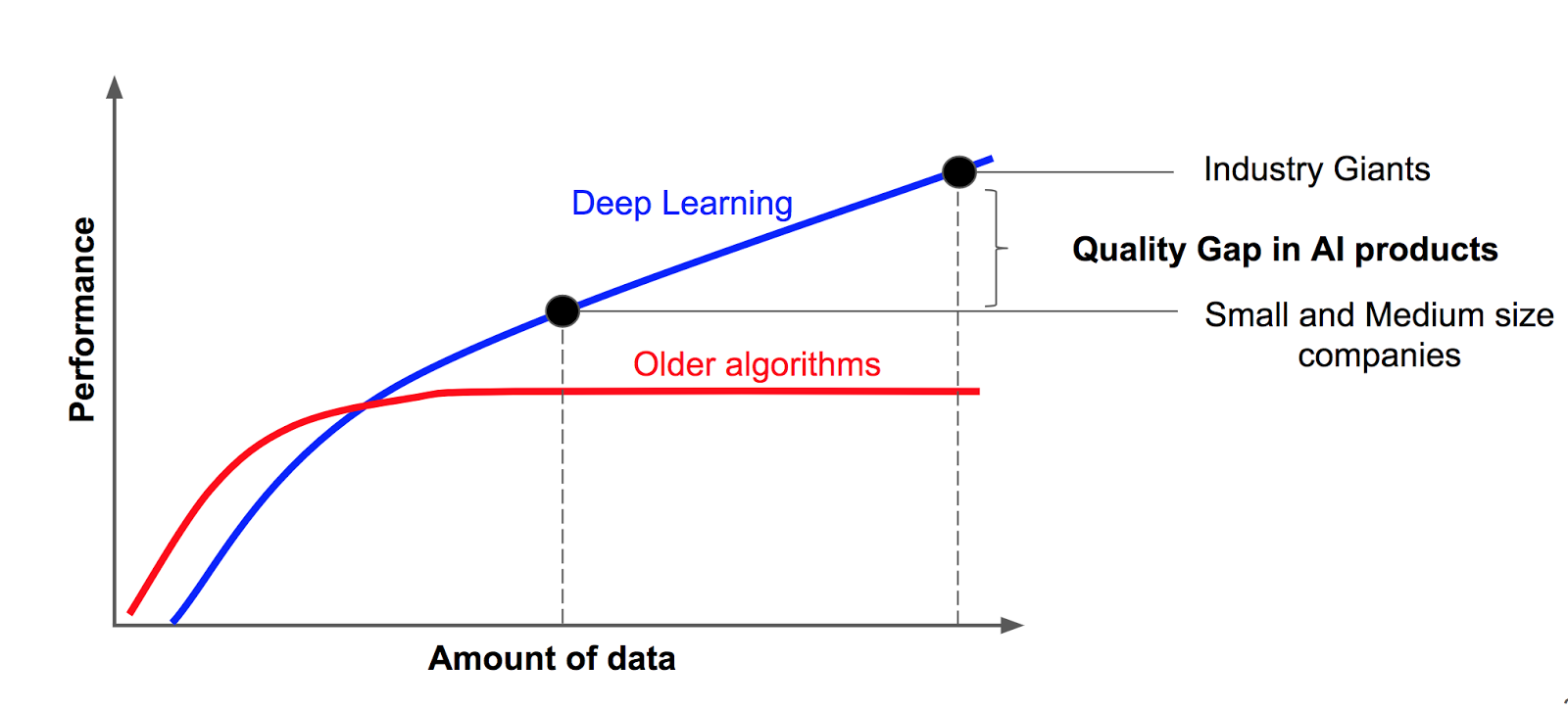
Читая о глубоких нейронных сетях, я часто сталкиваюсь с утверждением, что глубокое обучение эффективно только тогда, когда у вас есть большие объемы данных. Эти утверждения обычно сопровождаются таким рисунком:
Пример (взятый из https://hackernoon.com/%EF%B8%8F-big-challenge-in-deep-learning-training-data-31a88b97b282) приписывается “знаменитому слайду Эндрю Нга”. Кто-нибудь знает, на чем на самом деле основан этот рисунок? Есть ли какие-либо исследования, которые подтверждают это утверждение?
Оригинальный слайд “Масштаб определяет прогресс глубокого обучения”, возможно, можно найти по адресу https://cs230.stanford.edu/files/C1M1.pdf (страница 13). Его можно примерно интерпретировать как “модели с низким смещением [на этом графике, более крупные нейронные сети] тенденция получать выгоду от большего количества обучающих примеров“.
Основная причина заключается в том, что в глубоком обучении количество обучающих параметров настолько велико, и существует факт, что для каждого параметра вам нужно как минимум $5$ до $10$ данных для получения хорошего предсказания. Причина немного сложна для объяснения, но она связана с упаковкой обучения, и если вы настаиваете на том, чтобы узнать, почему, я могу сказать вам, что в ошибочном термине для тестовых данных у вас есть термин переобучения, который увеличивается с размером выборки, если ваша модель обучения представляет собой гипотезу, которая увеличивается, когда количество данных увеличивается. В гипотезе с ростом $O(2^n)$ невозможно сделать ошибку обобщения такой же, как ошибка обучения, например, 1NN. Напротив, гипотезы с ростом $O(n^c)$, которые ограничены полиномами, могут иметь переобучение, которое можно уменьшить, увеличив объем обучающих данных. Следовательно, если вы увеличите объем ваших данных, вы сможете добиться лучшей ошибки обобщения. Модели глубокого обучения подчиняются второму способу роста. Чем больше данных у вас есть, тем лучше у вас обобщение.
Глубокое обучение не требует уменьшения признаков для повышения точности. Глубокое обучение автоматически подавляет признаки, которые не способствуют точности результата. Большие данные представляют собой правила или функции в данных, называемые сигналом. Чем больше сигналов может быть обнаружено нейронной сетью глубокого обучения, тем выше ее точность.
Не многие люди рассматривали эту проблему с теоретической точки зрения. Существует направление исследований, сосредотачивающееся на выборе модели, которое может быть полезно рассмотреть.
Фон
Выбор модели переплетен с данными в стохастическом обучении. Традиционно есть два основных элемента, которые определяют, какая модель должна быть использована в зависимости от данных: тип модели и сложность. В обучении данные движут компонентом модели, в то время как сложность определяется тем, как она измеряется и архитектурой модели. Это все элегантный способ указать на то, что в сущности эквивалентно компромиссу между смещением и дисперсией. Следовательно, количество необходимых данных обычно насыщается в какой-то момент в процессе обучения, и это в значительной степени объясняется принципом компромисса между смещением и дисперсией и его зависимостью от сложности модели.
Глубокое обучение
Одно из наблюдений в области глубокого обучения заключается в том, что добавление большего количества данных, похоже, не приводит к насыщению. Это побудило некоторых людей пересмотреть представление о компромиссе между смещением и дисперсией. На самом деле оказывается, что для моделей глубокого обучения может быть верным, что наше традиционное представление о компромиссе между смещением и дисперсией больше не имеет силы. Я рекомендую вам прочитать [1], чтобы получить полное описание, а также [2].
Заключение
Вместо того чтобы ставить под сомнение глубокое обучение как некую необычную категорию модели, которая как-то жадно требует данных, было бы полезно задуматься о ограничениях нашего понимания выбора модели и его связи с данными.
Дополнительные ресурсы
[1] Belkin, M., Hsu, D., Ma, S., & Mandal, S. (2019). Примирение современной практики машинного обучения и классического компромисса между смещением и дисперсией. Труды Национальной академии наук, 116(32), 15849-15854.
[2] Dwivedi, R., Singh, C., Yu, B., & Wainwright, M. J. (2020). Повторный анализ сложности и компромисса между смещением и дисперсией. arXiv preprint arXiv:2006.10189.
Ответ или решение
Глубокое обучение и большой объем данных: происхождение правила
Введение
Глубокое обучение стало неотъемлемой частью современного искусственного интеллекта, позволяя достигать впечатляющих результатов в различных областях, включая компьютерное зрение и обработку естественного языка. Однако часто утверждается, что глубокое обучение требует больших объемов данных для эффективного обучения. Это правило, известное как «глубокое обучение требует больших данных», имеет свои корни в сложных механизмах обучения и структуре нейронных сетей. В этой статье мы подробно рассмотрим происхождение этого правила, его основания и последствия.
Причины, стоящие за правилом «глубокое обучение требует больших данных»
-
Структура нейронных сетей: Современные нейронные сети, особенно глубокие, характеризуются большим числом параметров. Каждая дополнительная пара нейронов, слой или соединение увеличивает количество весов, которые необходимо оптимизировать. Для того чтобы обучающая выборка обеспечивала надежные оценки весов нейронной сети, необходим объем данных, в 5-10 раз превышающий количество параметров. Этот принцип связан с концепцией преобладания «переобучения», при котором модель не в состоянии обобщить на новые данные.
-
Сложность моделей: Глубокое обучение относится к классу «низко смещенных» моделей, что означает, что они способны захватывать и моделировать сложные зависимости в данных. Однако, чтобы избежать переобучения, требуется значительное количество примеров для надежного представления обучаемой функции. Как правило, для глубоких нейронных сетей предполагается, что увеличение объема данных приводит к снижению обобщающей ошибки, подтверждая необходимость больших наборов данных для стабильного и точного обучения.
-
Необходимость для извлечения сигналов: Данные содержат «сигналы», которые нейронные сети должны выявлять и использовать для принятия решений. Большие объемы данных позволяют сети обнаруживать большее количество корреляций и шаблонов, тем самым повышая общую точность. В отличие от традиционных методов, глубокое обучение не требует предварительной обработки данных для выделения признаков, что позволяет моделям автоматически идентифицировать наиболее значимые характеристики в больших наборах данных.
-
Теория обучения: Исследования показывают, что в случае глубокого обучения традиционная концепция компромисса между смещением и дисперсией может не полностью применяться. Напротив, добавление большего числа данных часто продолжает улучшать производительность модели, что ставит под сомнение предопределенные лимиты, присущие более простым моделям.
Модельный отбор и зависимость от данных
Выбор модели — важный аспект, который тесно связан с объемом данных. В контексте глубокого обучения наблюдается явление, при котором добавление новых данных не приводит к насыщению результатов. Это открытие поставило под сомнение традиционные подходы к отбору моделей, предлагая новые пути для понимания взаимодействия между моделью, данными и сложностью.
Заключение
Правило о том, что глубокое обучение требует больших объемов данных, уходит корнями в сложные зависимости между нейронными сетями и числом их параметров. Научные исследования подтверждают тот факт, что большее количество данных увеличивает вероятность успешного обучения нейронной сети, уменьшая тем самым вероятность переобучения и повышая точность. Вместо того чтобы рассматривать глубокое обучение как исключительно «глубокую» научную дисциплину, важно осознать, что это также отражает ограничения нашего понимания взаимодействия модели и данных и продолжающееся развитие моделей в контексте больших данных.
Для тех, кто заинтересован в углублении понимания взаимосвязи между обучением, данными и чудесами глубокого обучения, рекомендуются следующие ресурсы: работы Belkin и др. по уравниванию современных практик машинного обучения с традиционными взглядами на смещение и дисперсию, а также исследования Dwivedi с коллегами, пересматривающие сложность и компромисс дисперсии.
Эта информированность помогает не только в теоретическом понимании, но и в практическом применении глубокого обучения в разнообразных областях, встретившихся сегодня с вызовами в обработке данных и точности прогнозов.