Почему изменение числа кластеров изменяет график в K-means?

Может быть, это глупый вопрос, но я не могу найти на него ответ. У меня нет идеального математического понимания kmeans, так что прошу прощения, если это так.

Мне просто интересно, почему я вижу другой график, когда изменяю количество кластеров в графике kmeans?

Вот код, который я использую:

set.seed(1)
k <- kmeans(data, centers = x)
plotcluster(data, k$cluster)

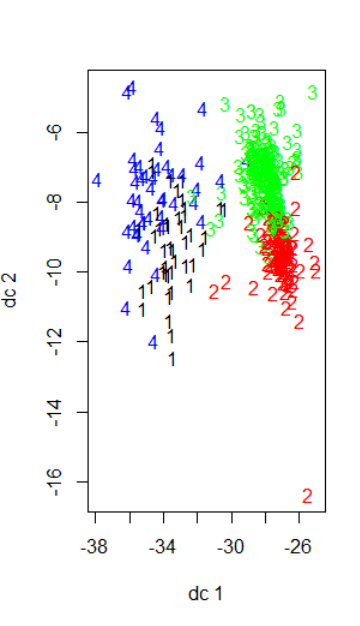
Я варьирую x, чтобы посмотреть, как выглядит график. Ниже приведены результаты для x = 3 и x = 4. Извините за плохое форматирование.

Мне интересно, почему оба графика выглядят по-разному, если я только изменяю количество кластеров. Это связано с тем, что главные компоненты, которые показываются, dc1 и dc2, различаются, когда вы изменяете x, чтобы максимизировать отображаемую дисперсию?

Еще один быстрый вопрос: можно ли определить номер кластера по тому, насколько “аккуратным” выглядит кластеризация на графике? Я знаю, что есть различные методы для этого, просто интересно, является ли график показателем хорошей/плохой кластеризации.

Любая помощь будет оценена!

plotcluster изменяет проекцию в зависимости от результата, который вы задаете. См. документацию для получения дополнительной информации.

Из-за этого вы не можете сравнивать два графика.

Основы kmeans заключаются в формуле расстояния, она пытается удерживать точки данных как можно ближе друг к другу итеративно. Поэтому, когда вы увеличиваете количество своих кластеров, она пытается создать разные центроиды (центр кластера), а затем пытается найти ближайшие возможные точки данных. Таким образом, у вас разные типы графиков каждый раз, когда вы увеличиваете количество n. Также имейте в виду, что цвета могут варьироваться в зависимости от типа графика, который вы используете, и каждый раз они будут разными.

Таким образом, сравнивайте разные графики с n = 3, сравнивать n = 3 и 4 неправильно, если вы хотите проводить сравнение на основе цветов и форм. Поскольку теперь у них разные центроиды, и в вашем случае вы можете увидеть, что 1-й и 4-й кластеры на 2-м изображении пересекаются друг с другом. Обратите внимание и на это, возможно, они неправильно кластеризуются 1-й и 4-й.

Я полагаю, вы, возможно, спрашиваете, почему расположение точек данных на визуализации k-means меняется, когда входные данные в обоих случаях одинаковы, только значение k меняется.

Кластеризация работает в k-мерном пространстве, где k – это количество кластеров. Она использует входные данные для отображения каждой точки данных в новую точку с k-измерениями.

Тем не менее, k-мерные пространства нельзя графически изобразить на прямоугольнике, когда $k \gt 2$, или на кубе, когда $k \gt 3$. Чтобы позволить визуализацию, plotcluster проецирует k-мерное пространство в 2-мерное пространство, а затем представляет измерения в цвете. Поскольку k-мерные точки данных были разными, визуализированные 2-мерные точки данных также различаются.

почему я вижу другой график, когда изменяю количество кластеров в
графике kmeans?

Кластеризация каждой наблюдения в кластеризации k-Means зависит от количества кластеров (центроидов), которые вы выбираете. Их центроиды самостоятельно настраиваются, итеративно выполняя алгоритм, так что положение каждого из них зависит от положения других. Вот почему введение нового центроида сдвигает другие к новому равновесию.

—

можно ли определить номер кластера по тому, насколько “аккуратным” выглядит кластеризация на
графике?

Общий способ выбора их числа – использовать метод локтя. Он основан на повторении алгоритма многократно, каждый раз с разным k, проверяя количество информации/ошибки, которые возвращает каждая кластеризация. Посмотрев на график этих итераций, вы можете выбрать количество кластеров, которое вас удовлетворяет.