Вопрос или проблема
Мне было интересно, почему в интернете нет точного изображения функции активации softmax. Это сложно для построения графика или в чем причина этого, так как я хочу сравнить ее с сигмоидной функцией?
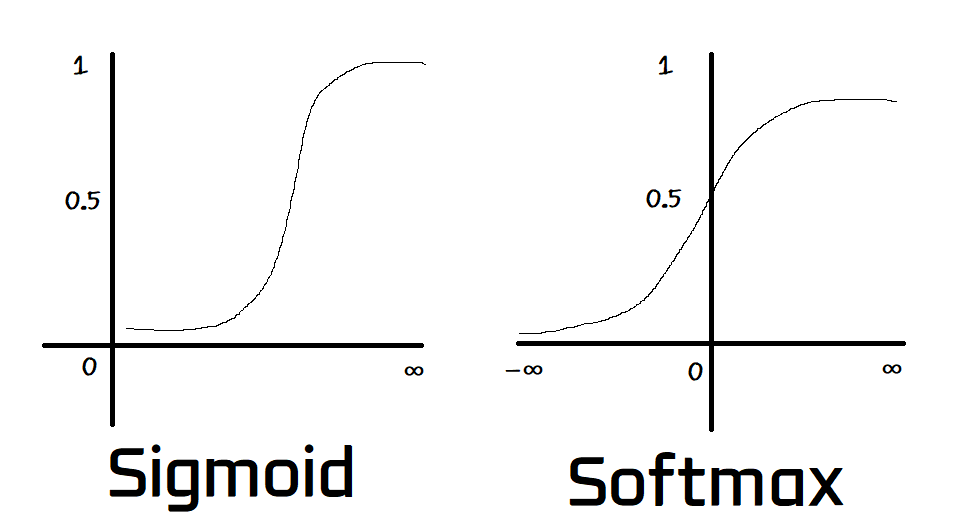
Я только что нашел следующие забавные картинки с dataaspirant, которые больше недоступны:

Может ли кто-то проиллюстрировать график функции Softmax? и объяснить, почему одна быстрее другой на основе приведенной выше картинки?
Softmax, как правило, является многопеременной функцией. Вы не взяли бы softmax от одной переменной, так же как вы не взяли бы максимальную величину от одной переменной. Сложно построить графики функций более чем двух переменных, потому что наши глаза видят в трех измерениях.
Сигмойда – это одномерная функция. На вашей картинке они применяют сигмоиду к каждой переменной отдельно.
Softmax не является непрерывной математической функцией, такой как логистическая (сигмоидная), tanh или ReLU. Она используется для отображения выходов последнего слоя нейронной сети в вероятностное распределение, т.е. сумма выходов сжатого слоя softmax будет равна 1 (единица).
В отличие от других функций активации softmax принимает список/массив входных данных и отображает их в вероятностное распределение.
Пример: softmax([ 2.0 , 1.0 , 0.1 ]) вернет [ 0.7 , 0.2 , 0.1 ]
И 0.7 + 0.2 + 0.1 = 1, так что если мы передадим в softmax список с только одним элементом, его вероятность возникновения будет 1 (единица), т.е. softmax([ любое_значение ]) вернет 1.
Поэтому softmax полезна только тогда, когда нужно сжать несколько выходов.
function softmax(list){
// list это массив выходов нейронов последнего слоя нейронной сети
// numerators это массив Math.exp(), примененного к каждому элементу массива list
var numerators = list.map(function(e){ return Math.exp(e); });
// denominator это сумма каждого элемента массива numerators
var denominator = numerators.reduce(function(p, c){ return p + c; });
// возвращает массив numerators, после деления каждого элемента на denominator
return numerators.map(function(e){ return e / denominator; });
}
Softmax полезна в задачах классификации.
Функция softmax используется на последнем слое сети CNN. Softmax – это функция активации как tanh и ReLU, разница в том, что эта техника может интерпретировать входные значения как вероятности выхода. Метод гарантирует, что вероятности выхода будут находиться в диапазоне от 0 до 1, и их сумма будет равна 1, таким образом, результаты могут интерпретироваться как процентное отношение для каждого класса. Функция использует эту формулу, также вы можете использовать эти строки кода для вычисления softmax:
logits = [2.0, 1.0, 0.1]
exps = [np.exp(i) for i in logits]
sum_of_exps = sum(exps)
softmax = [j/sum_of_exps for j in exps]
print(softmax)
Я опоздал на свою вечеринку…
в общем, возможно построить после реализации функции активации Softmax, однако она может варьироваться, потому что:
Функция softmax сильно отличается от других функций активации (AF), потому что она работает с вероятностью. вкратце:
….которая превращает числа, также известные как logits (числовой выход последнего линейного слоя многоклассовой нейронной сети), в вероятности, которые суммируются до 1. Функция softmax выдает вектор, представляющий распределение вероятностей по списку возможных исходов. ref.
 автор изображения, которое также может быть связано с другой функцией потерь кросс-энтропии.
автор изображения, которое также может быть связано с другой функцией потерь кросс-энтропии.
Это распределение вероятностей по N количеству классов. Эта функция активации обычно применяется к концу нейронной сети, где мы хотим, чтобы она вычисляла вероятность.
 |
|---|
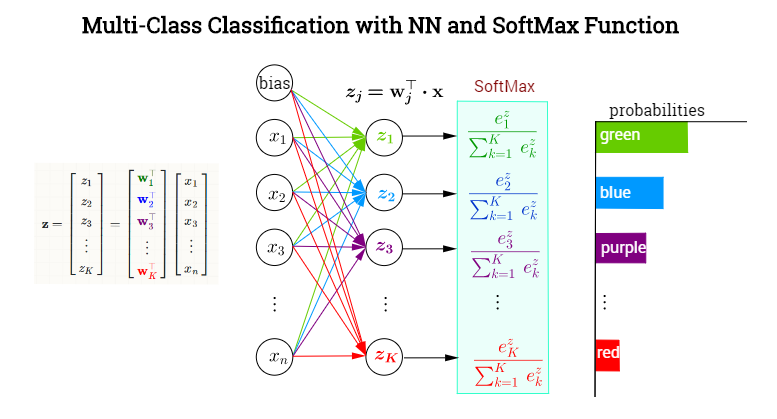
| Рис. 1: Понимание функции активации. ref |
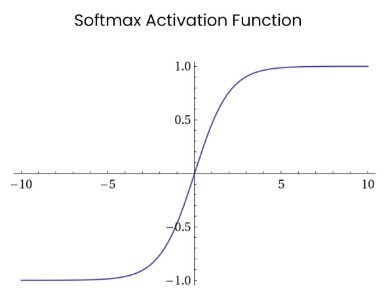
Я нашел хорошую статью, диаграммы и сравнение результатов обеих функций активации, можно увидеть, что нет большой разницы между графиками сигмоидной функции и графиком функции softmax:
 |
 |
|---|---|
| Рис. 2: Функция активации Softmax объяснена с кодом (Go) Понимание почему и как использовать функцию активации softmax. ref | Рис. 2: Сравнение между выходами сигмоиды и softmax:. ref |
Помимо некоторых связанных постов: пост 1 , пост 2, есть некоторые посты, которые объясняют эту функцию активации эксклюзивно:
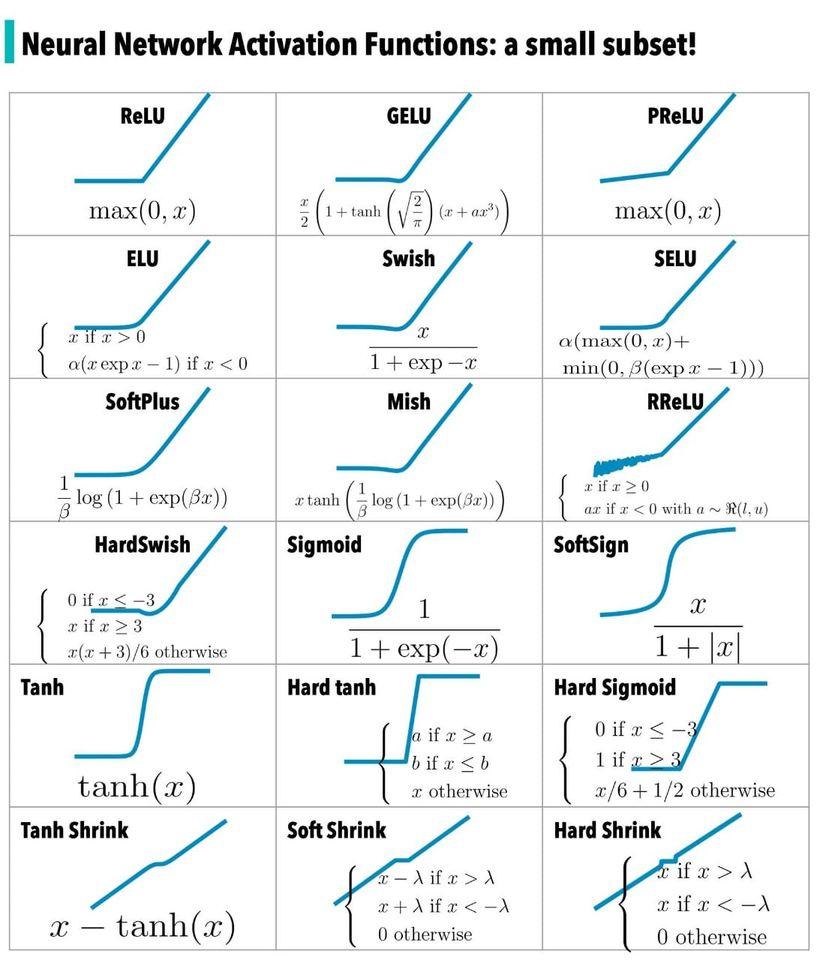
Интересно, что я нашел различные графики функций активации в нейронных сетях, включая Софт-… из источника FB, который кто-то поделился, и который я хотел бы поделиться здесь из-за прекрасного видения, которое может дать этот пост:
- СофтПлюс
- СофтЗнак
- СофтШринк
.
Ответ или решение
Функция softmax, хотя и чрезвычайно важна в области машинного обучения и глубинного обучения, действительно трудно поддается визуализации по сравнению с другими активационными функциями, такими как сигмоида. Давайте рассмотрим, почему это так, и обсудим особенности и применение функции softmax.
### Теория
Функция softmax представляет собой особую активационную функцию, которая преобразует вектор чисел (обычно это логиты, выходы последнего линейного слоя нейронной сети) в вероятностное распределение. Особенность этой функции заключается в том, что она преобразует значения логитов таким образом, чтобы их сумма равнялась единице. Она обеспечивает нормировку, обеспечивая при этом интерпретацию значений как вероятностей принадлежности к различным классам. Алгоритмически функция определяется следующим образом:
$$\text{Softmax}(z_i) = \frac{e^{z_i}}{\sum_{j=1}^{N} e^{z_j}}$$
где $z_i$ – логит для класса $i$, а $N$ – общее число классов. Это уравнение показывает, как экспоненциальные функции числителей нормализуются суммой всех экспонент вектора.
### Пример
Рассмотрим случай применения функции softmax к массиву логитов, например, [2.0, 1.0, 0.1]. Для каждого элемента массива сначала вычисляется экспонента, и далее каждый из этих экспонент делится на сумму всех экспонент:
1. Вычислить экспоненциальные значения: $$e^{2.0}, e^{1.0}, e^{0.1}$$.
2. Суммировать экспоненциальные значения.
3. Разделить каждое экспоненциальное значение на полученную сумму, что даст вероятности: [0.7, 0.2, 0.1].
На этом примере класс с наибольшим значением логита (2.0) получает наибольшую вероятность (0.7).
### Применение
В отличие от таких активационных функций, как сигмоида или ReLU, которые применяются элементарно к каждому отдельному узлу, softmax применяется ко всему вектору. Это делает функцию более сложной для визуализации как графика. Сигмоида, например, мономерно повышает одно значение, придерживаясь схемы S-образной кривой, и ее можно легко представить в двух измерениях с фиксированной осью x. Softmax, работая с векторами, требует многомерной визуализации, представляя каждый из выводов как отдельную вероятность.
Она не только приводит логиты к вероятностям, но и выполняет более сложные операции, связанные с отношениями между классами. Поэтому в задачах классификации, особенно когда работает многоклассовая модель, softmax устраняет необходимость в нескольких бинарных классификаторах и позволяет решать задачу с помощью одной универсальной функции.
Кроме того, в процессе обучения глубоких нейронных сетей softmax часто используется в качестве последнего слоя, что позволяет интегрировать его результаты напрямую в функции потери, такие как кросс-энтропия.
### Заключение
Хотя нет единой формы для графического изображения softmax, именно ее высокая размерность и необходимость отображения векторов вероятностей делают эту функцию уникальной. Ориентируясь на отношение между классами и обеспечивая корректные вероятности, softmax продолжает оставаться хранителем сложных многоклассовых систем.
Сравнение с сигмоидой показывает существенно различные подходы к обработке данных: одна вносит ясность в бинарную классификацию через элементарное скалярное умножение, другая – предлагает гармоничный путь для многомерного распределения вероятностей. Эти различия подчеркивают узкое, но важное место каждой функции в нейронных сетях.