Вопрос или проблема
Я работаю над проектом, связанным с подгонкой плоскостей к 3D облакам точек. Часть, отвечающая за подгонку плоскостей, работает хорошо, но я пытаюсь определить лучший способ ограничить подогнанные плоскости данными точками, к которым они подходят. Мне нужны ограниченные регионы плоскостей, а не просто их уравнения, поэтому я должен решить, какие точки в наборе данных «принадлежат» какой плоскости после процесса подгонки. Плоскости ориентированы более или менее случайно и могут пересекаться, что усложняет задачу.
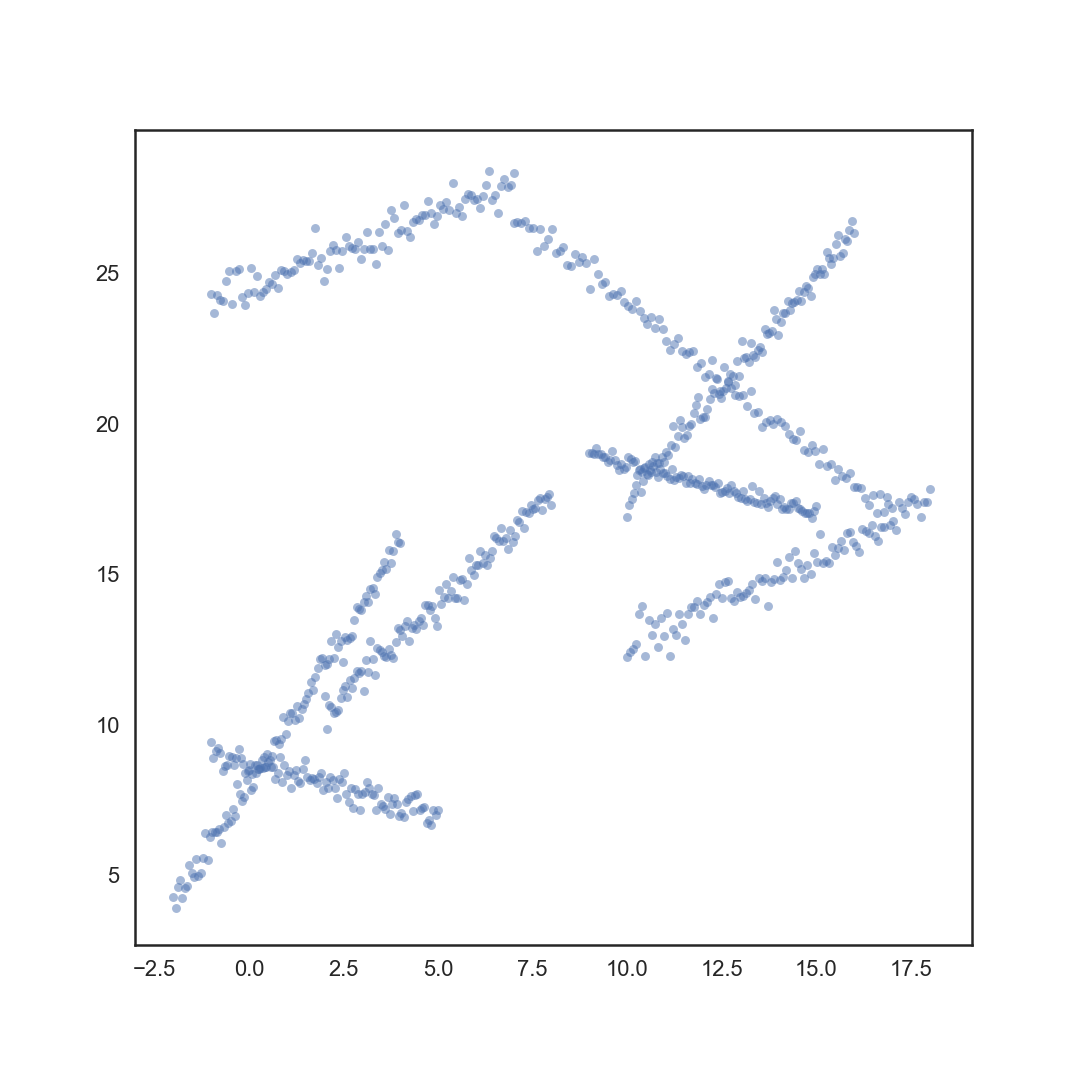
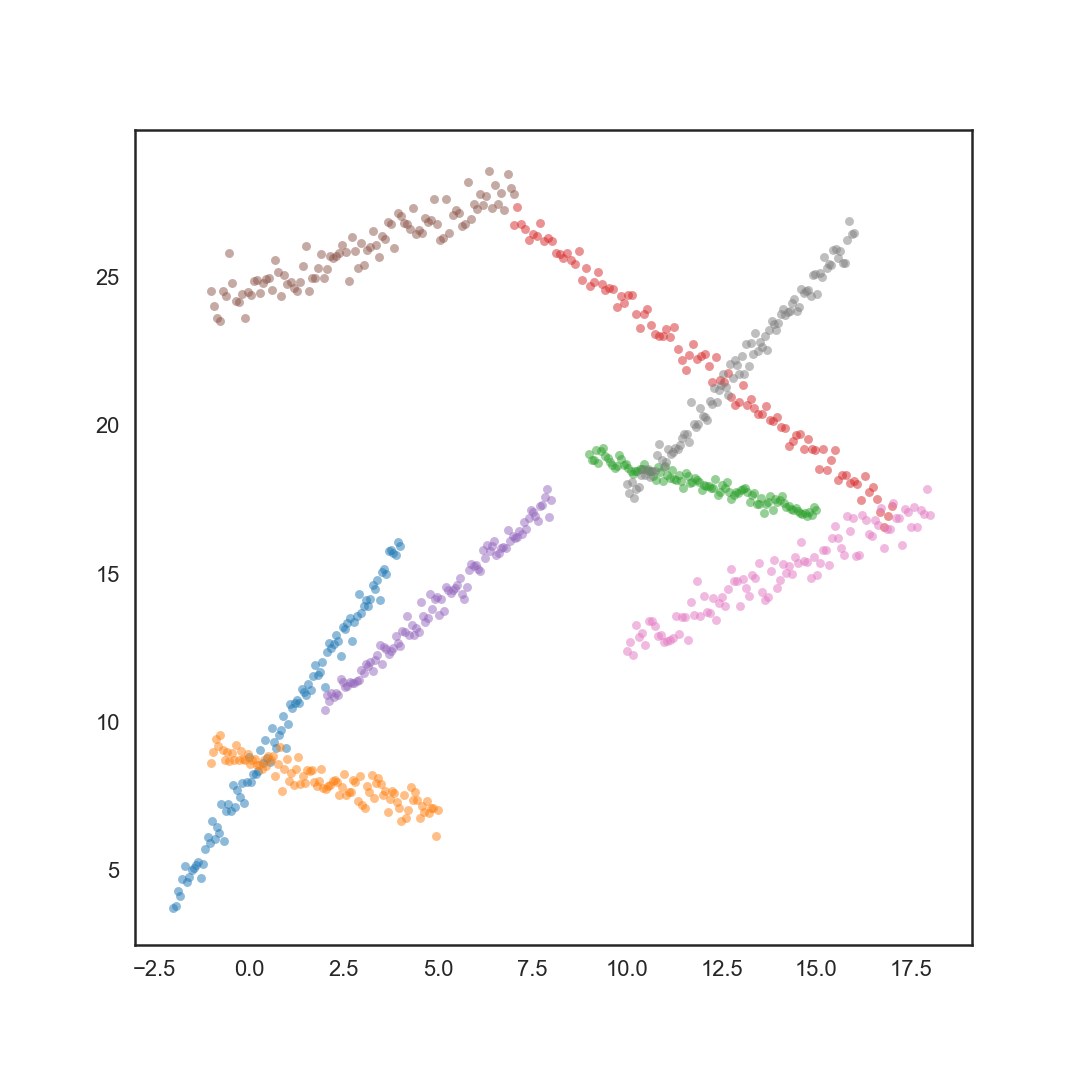
Это легче представить в 2D с линиями вместо плоскостей, поэтому я сделал два примера графиков. Первый содержит необработанные данные синим цветом. Я могу найти уравнения линий, которые соответствуют линейным кластерам данных. Исходя из этих уравнений, я хочу получить выделенные кластеры на втором графике. У меня есть что-то рабочее, использующее расчет текучести дисперсии и беру все точки, которые находятся ниже некоторого порога, но это не идеально, и я знаю, что должно быть гораздо лучший способ сделать это. У меня есть ощущение, что мне нужен алгоритм, который учитывает геометрию кластеров, а не только расстояние от каждой точки до плоскости. Взятие всех точек в пределах некоторого порогового расстояния от каждой плоскости проблематично по нескольким причинам, поэтому я ищу что-то лучшее, чем это.
Один из вариантов – это двухступенчатый процесс:
-
Использовать спектральную кластеризацию для нахождения групп. Поскольку спектральная кластеризация основана на графах, она хорошо находит связанные группы.
-
Для каждого кластера индивидуально оценить ограниченные регионы плоскостей. Это часто называют выпуклой оболочкой.
Ответ или решение
Присвоение точек подогнанным плоскостям в 3D
Работа с облаками точек в 3D и подгонка к ним плоскостей представляет собой сложную задачу, особенно когда требуется четко определить, какие точки принадлежат конкретным плоскостям. Ваша текущая реализация, основанная на расчете локальной дисперсии, имеет свои ограничения, так как вы уже отметили, и позволяет рассмотреть более надежные методы, которые учитывают геометрические особенности кластеров.
1. Спектральная кластеризация
Первый шаг в вашем предложении — применение спектральной кластеризации. Этот метод эффективен для поиска связанных групп точек, что особенно полезно в случае случайной ориентации плоскостей и их возможного пересечения. Спектральная кластеризация работает на основе построения графа, где точки являются вершинами, а связи между ними — ребрами, что позволяет выделить естественные сообщества в данных.
Подход
- Построение графа: Каждой точке сопоставляется близость к другим точкам, что позволяет выявить связи внутри данных.
- Собственные векторы: Используя собственные векторы матрицы смежности, можно определить низкоразмерное представление, которое выделяет кластеры.
- Кластеризация: Применение алгоритму, такого как K-Means, на результирующих векторах позволяет выделить группы.
2. Определение ограниченных регионов (Конвексные оболочки)
Вторым этапом вашего подхода является определение ограниченных регионов для каждой группы. Это можно сделать с использованием алгоритма вычисления конвексной оболочки. Данный метод позволяет получить наименьшую выпуклую оболочку, содержащую все точки из кластера.
Подход
- Метод Грэхема или алгоритм Джарвиса: Это классические алгоритмы для построения конвексной оболочки множества точек.
- Проверка принадлежности: Каждая точка из облака будет проверяться на принадлежность к сформированной конвексной оболочке, что даст четкое представление о том, какие точки принадлежат к конкретной плоскости.
Заключение
Использование спектральной кластеризации для выделения групп точек в сочетании с алгоритмом вычисления конвексной оболочки предоставляет вам мощный инструмент для работы с подогнанными плоскостями. Эти методы учтут геометрические особенности кластеров и позволят минимизировать воздействие пересечений между плоскостями. Рекомендуется также проводить визуализацию полученных результатов на графиках, чтобы убедиться в корректности и целостности данных.
Ключевые слова для SEO: 3D облака точек, подгонка плоскостей, спектральная кластеризация, конвексная оболочка, геометрические методы кластеризации.
Ваш дальнейший успех будет зависеть от тщательной настройки и тестирования предложенных методов на вашем наборе данных. Удачи в вашем проекте!