Вопрос или проблема
Я нашел рекурсивную версию прямого алгоритма на Википедии, однако я не понимаю обозначения, использованные в псевдокоде:
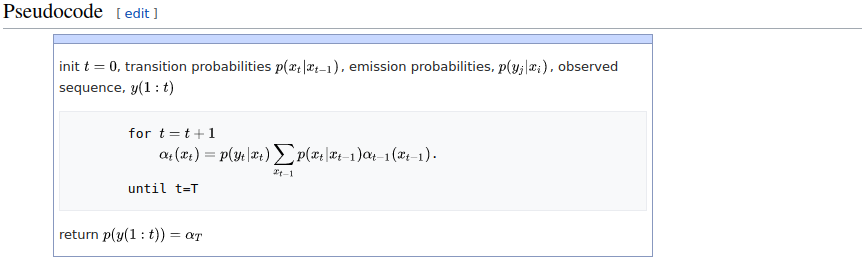
Что означает $$x_{t-1}$$ под знаком суммы? Что нужно суммировать?
Было бы очень полезно, если бы кто-нибудь мог предоставить пример расчета.
Спасибо!
У нас есть последовательность наблюдений $x_1, x_2,…,x_T$, поэтому $x_{t-1}$ это просто
наблюдение непосредственно перед $x_t$ (для любого $t>0$).
При симуляции прямого алгоритма полезно составить таблицу, где $T$ (число наблюдений) — это количество столбцов, а количество строк равно количеству возможных меток. Каждая ячейка $(t,y)$ в этой таблице в конечном итоге будет содержать вероятность наличия метки $y$ в момент времени $t$. Таблица заполняется столбец за столбцом, начиная с левого, то есть сначала инициализируются все метки при $t=0$. Затем для каждого столбца расчет зависит только от предыдущего столбца (благодаря предположению независимости).
Вы можете найти подробное объяснение в этой книге, например.
Ответ или решение
Понимание алгоритма продвижения для скрытых марковских моделей (HMM) требует глубины как в теоретическом подходе, так и в его практическом применении. По сути, алгоритм продвижения — это динамический программный метод для вычисления вероятности наблюдения определенной последовательности в контексте скрытой марковской модели.
Теория (T)
Скрытая марковская модель описывает вероятностную структуру, состоящую из скрытых состояний и наблюдаемых событий. Для каждого временного интервала наблюдения происходят с определенной вероятностью, зависящей от текущего скрытого состояния.
Алгоритм продвижения используется для оценки наблюдаемой последовательности. Он вычисляет вероятности, комбинируя начальные вероятности, вероятности перехода между скрытыми состояниями, и вероятности эмиссии, характеризующие вероятность наблюдений при условии скрытого состояния.
Notation in the pseudocode, particularly under the summation sign like (x_{t-1}), refers to the hidden state at the previous time step. In essence, you sum over all possible previous states to account for all potential transitions.
Пример (E)
Рассмотрим последовательность наблюдений (O = (o_1, o_2, … , o_T)) и множество скрытых состояний (S = (s_1, s_2, … , s_N)).
-
Инициализация: Вычисляется начальная вероятность нахождения в каждом скрытом состоянии (s_i) с учетом первого наблюдения (o_1).
[
\alpha_1(i) = \pi_i \cdot b_i(o_1)
]
где (\pi_i) — начальная вероятность состояния (s_i), а (b_i(o_1)) — вероятность наблюдения (o_1) в состоянии (s_i). -
Рекурсия: Для каждого последующего наблюдения (o_t) (при (t=2) до (T)) рекурсивно вычисляется вероятность:
[
\alphat(j) = \left( \sum{i=1}^N \alpha{t-1}(i) \cdot a{ij} \right) \cdot b_j(ot)
]
Здесь (\alpha{t-1}(i)) — вероятность последовательности наблюдений до момента времени (t-1) в состоянии (si), (a{ij}) — вероятность перехода из состояния (s_i) в состояние (s_j), и (b_j(o_t)) — вероятность наблюдения (o_t) в состоянии (s_j). -
Терминация: Устанавливается суммарная вероятность наблюдаемой последовательности.
[
P(O|\lambda) = \sum_{i=1}^N \alpha_T(i)
]
Применение на практике (A)
Чтобы применять алгоритм в реальных сценариях, создается таблица, где каждая строка соответствует возможному скрытому состоянию, а столбцы — временным шагам последовательности наблюдений. По мере продвижения расчета, заполняется таблица вероятностей (\alpha_t(j)).
Практическим применением алгоритма продвижения может быть, например, распознавание речи, где набор звуков представляется как последовательность наблюдений, а слова — как скрытые состояния. При помощи алгоритма определяется вероятность последовательности звуков, условно на набор возможных слов, что позволяет улучшить качество распознавания.
Помимо теоретических разработок, для более глубокого понимания и примеров вы можете обратиться к ресурсам, таким как книги и учебные материалы, упомянутые в вашем вопросе.