Вопрос или проблема
Я создал модель для прогнозирования вне выборки, которая использует многошаговую рекурсивную стратегию, чтобы свести мою задачу к регрессии. Прогнозы достаточны, но я задумался, есть ли возможность добавить что-то вроде интервалов прогнозирования – я знаю, как это сделать, используя решения на основе остатков (например, RMSFE) только для моделей в выборке, когда доступны исторические данные.
Я читал где-то об идее использования байесовского структурного моделирования временных рядов для прошлых ошибок прогнозирования, чтобы как-то оценить неопределенность, а затем метод Монте-Карло для генерации диапазона возможных будущих ошибок, но у меня есть некоторые сомнения относительно этого решения.
Мы можем построить Интервалы Прогнозирования (PIs) после получения набора прогнозов.
- Метод 1: RMSFE (Среднеквадратичная ошибка прогнозирования)
RMSFE похож на RMSE. Единственное отличие в том, что RMSFE нужно рассчитывать на остаточных терминах из прогнозов по невидимым данным (например, на валидационном или тестовом наборе).
-
Метод 2: BCVR (Бутстрэппинг Остатков Кросс-Валидации), который является теоретическим методом, предложенным Бренданом Артли в его онлайн статье:
- Прогнозирование временных рядов: Интервалы прогнозирования
Оценка диапазона будущего наблюдения с уверенностью
- Прогнозирование временных рядов: Интервалы прогнозирования
Примечание: Метод BCVR является теоретическим предложением, он еще не официальный. Пожалуйста, перепроверьте, если вы хотите использовать его в научных публикациях. Я не нашел официальной статьи на эту тему. На данный момент существует препринт статьи под названием “Бутстрэппинг Оценки Кросс-Валидации” от Браяна Цая и др.
Все, что мне знакомо, это методы, основанные на остатках прошлых временных меток (например, RMSFE). Можно ли как-то включить их в будущие временные метки?
Да, это можно достичь, используя Рекурсивную многошаговую стратегию прогнозирования, которая изображена на следующем рисунке:
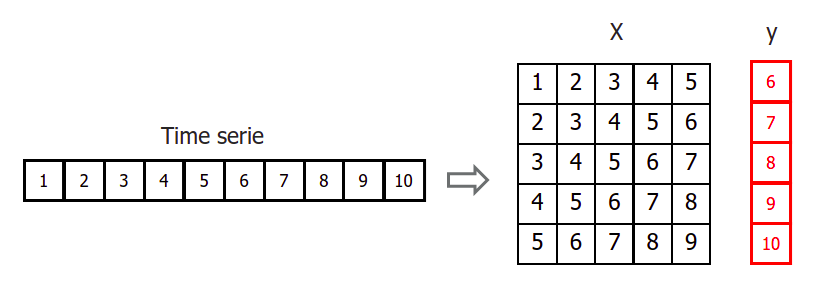
Вы можете использовать пакет skforecast и работать с классами ForecasterAutoreg & ForecasterAutoregCustom согласно документации
Также вы можете установить regressor = lightgbm.LGBMRegressor() из lightgbm документации при желании.
Я достиг этих результатов, используя RMSE; вы можете изменить его и использовать вышеупомянутые методы. Вы можете расширить это:
-
для RMSFE следующим образом:
RMSFE = np.sqrt(sum([x**2 for x in residuals]) / len(residuals)) band_size = 1.96*RMSFE -
для BCVR проверьте предложенную реализацию автора
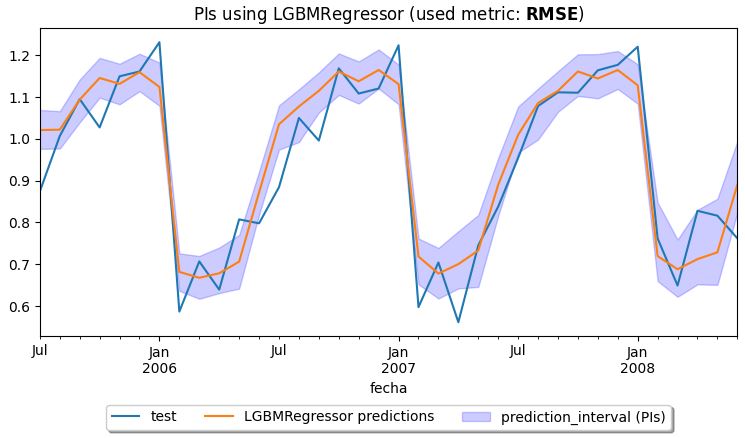
Вы можете воспроизвести, что я достиг, используя этот пример; в противном случае, дайте мне знать.
Ответ или решение
Предсказательные интервалы для будущих временных меток в контексте прогнозирования временных рядов представляют собой важный аспект анализа неопределенности. Ваш запрос на создание модели для прогноза вне выборки, использующей многошаговую рекурсивную стратегию, свидетельствует о стремлении учесть неопределенность прогнозов.
Теория (Theory):
Прогнозирование временных рядов само по себе не является легкой задачей, поскольку многие временные ряды содержат значительную степень стохастической неопределенности. Предсказательные интервалы помогают выразить эту неопределенность в виде диапазона, в котором с определенной вероятностью находится будущая наблюдаемая величина. Эти интервалы обычно строятся на доверительном уровне (например, 95%), показывая диапазон значений, которые, вероятно, включают в себя истинное значение.
На практике существует несколько методов для определения предсказательных интервалов. Один из основных методов — использование остаточных ошибок модели, таких как RMSFE (Root Mean Squared Forecasting Error), который аналогичен RMSE, но применительно к прогнозам на данных, не участвующих в обучении. Другой теоретически предлагаемый метод — BCVR (Bootstrapping Cross-Validation Residuals), который был предложен Бренданом Артли в его онлайн-статье. Хотя метод BCVR ещё не получил широкого признания в научной среде и не утвержден официально, он показывает интересные перспективы.
Примеры (Example):
-
RMSFE: Этот метод основывается на измерении среднеквадратической ошибки предсказания на данных, не использовавшихся при обучении. Это метод уменьшает влияние переобучения и обеспечивает более реальные оценки неопределенности.
RMSFE = np.sqrt(sum([x**2 for x in residuals]) / len(residuals)) band_size = 1.96 * RMSFEЗдесь
band_sizeможет быть использован для построения интервала вокруг прогнозов, чтобы учесть прогнозируемую неопределенность. -
BCVR: Этот метод использует бутстрепинг для моделирования распределения ошибок в кросс-валидации, что позволяет понять, как ошибки распределяются при различных гипотетических выборках.
Применение (Application):
-
Recursive Multi-Step Forecasting: Один из распространенных подходов к многошаговому прогнозированию заключается в использовании рекуррентных стратегий. Это значит, что мы создаем прогноз на следующий шаг на основе предыдущего прогноза, а не реальных значений. Подход схож с autoregressive моделями, где каждый элемент прогноза зависит от предыдущих.
-
skforecast пакет: Для облегчения реализации подобных стратегий вы можете использовать библиотеки, такие как
skforecast. Этот пакет предоставляет инструменты и классы, такие какForecasterAutoregиForecasterAutoregCustom, которые интегрируются с различными регрессорами, включаяlightgbm.LGBMRegressor. Использование таких инструментов значительно упрощает реализацию прогностических алгоритмов и их тестирование. -
Расширение RMSFE или BCVR: Используйте предложенные методы для построения ваших предсказательных интервалов. Например, RMSFE может дать понимание диапазона ошибок прогноза, на основе чего можно строить интервалы с учетом доверительных уровней.
-
Инструменты в реальной практике: Если вы хотите воспроизвести похожие результаты, можно обратиться к общественным репозиториям или руководствам, чтобы получить примеры реализации. Например, пример реализации через
skforecastдоступен в официальной документации.
Заключение:
Создание предсказательных интервалов требует не только понимания теоретической базы, но и внимательного подхода к выбору методов в зависимости от специфики ряда и доступных данных. Необходимо также учитывать сложность используемых методов и их применимость в конкретных условиях, особенно при ограниченном количестве данных или высокой их изменчивости. Внимательное моделирование и работа с остатками ошибок прошлого помогут более уверенно прогнозировать будущее и строить надежные интервал-оценки.