Восстановление целочисленной функции с помощью *-обучения

У меня следующая проблема. Из технической модели у нас есть функция $f(n,p)$, приближающая время выполнения. Функция $f$ отображает

$$
f: \mathbb{N} \times \mathbb{P} \to \mathbb{R}_{+}
$$
где $\mathbb{P} = \{1,\ldots,50\} \subset\mathbb{N}$. $n$ определяет объем входных данных, а $p$ является параметром процесса, который имеет непрерывное влияние на время выполнения. Нас интересует значение $p$ такое, что $f(n,p)$ для заданного $n$. Во время эксперимента мы тестируем некоторые значения $n$, такие как 500, 1000, 5000, и для всех возможных значений $p$, а затем вручную выбираем оптимальное $p$. Например, для всего, что меньше 750, используйте оптимальное $p$ из тестового прогона с $n=500$ и так далее. Обычно для фиксированного $n$ время выполнения по $p$ имеет следующий характер, но с добавлением шума:

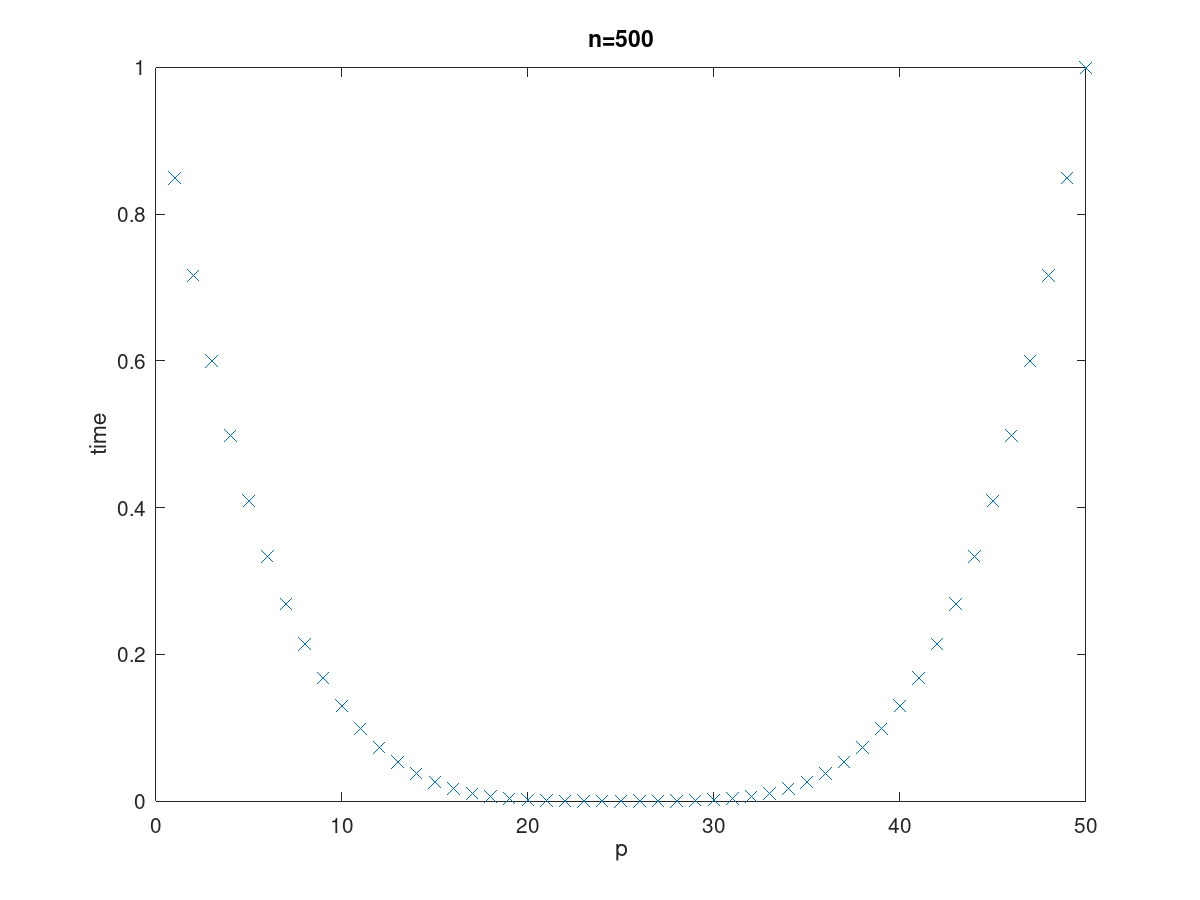
С увеличением $n$ дно сдвигается вправо, и из-за шума дно не плоское. Таким образом, в примере оптимальное $p$ находится где-то между $20$ и $30$.

Теперь мы ищем функцию $g$:

$$
g: \mathbb{N} \to \mathbb{P}
$$
которая определяется как
$$
g(n) = \operatorname{argmin}\limits_{p\in\mathbb{P}} f(n,p)
$$

Поскольку выборка $f$ для фиксированного $n$ не является проблемой, и у меня уже есть большой набор выборок, я считаю, что это будет хорошей задачей для начала изучения области машинного обучения для себя.

Мой основной вопрос в том, с чего начать? Ищите руководство по машинному обучению, я в основном наталкиваюсь на примеры распознавания изображений и не вижу никаких хороших связей между ними и моей проблемой.
Есть ли предложения, что почитать для решения этой проблемы? Какое программное обеспечение использовать? И, наконец, как извлечь $g$ таким образом, чтобы мы могли предоставить эту функцию пользователям или реализовать где-то? На данный момент я знаю, что $g$ является неубывающей для увеличивающегося $n$.

Редактировать
Результаты выборки могут также выглядеть вот так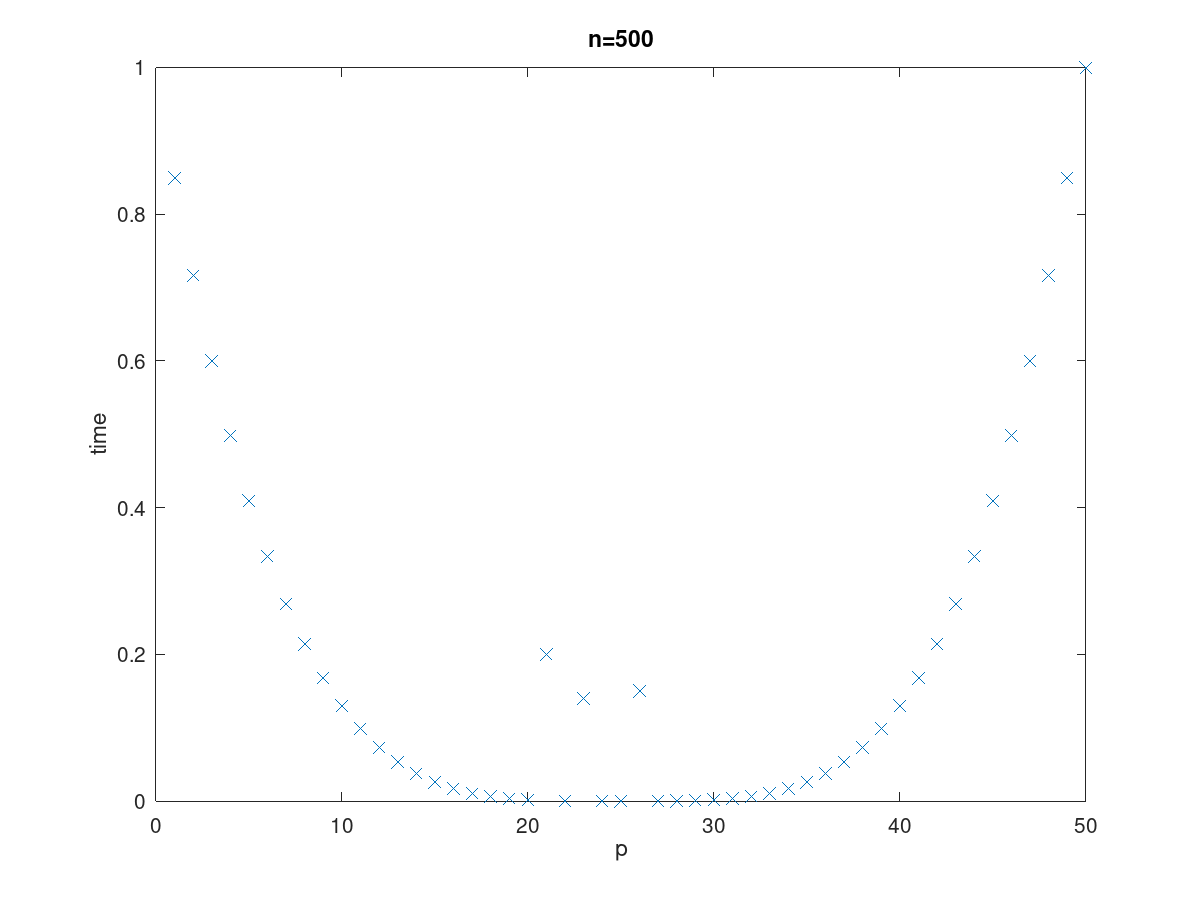

Таким образом, пики в области “минимальной” точки не являются шумом. Они вызваны техническими внутренностями рассматриваемого процесса. Таким образом, обрабатывая данные и удаляя шум, эти точки необходимо сохранить. И они делают нахождение $g$ таким сложным, потому что в одном прогона выборки минимальное $p$ лежит слева, в середине или справа от них. По этой причине я решил, что это будет хорошей точкой для использования машинного обучения, чтобы получить некоторые инсайты.

Если я правильно понимаю, цель будет состоять в том, чтобы модель получала значение $n$ и предсказывала оптимальное $p$, которое минимизирует $f(n,p)$.

С этой точки зрения это похоже на простую задачу регрессии. Вы, вероятно, могли бы обучить модель регрессии: для каждой точки в вашем наборе данных предиктором является $n$, а отклик — значение $p$, которое минимизирует $f(n,p)$ для этого $n$. Обратите внимание, что все точки, которые не соответствуют минимуму, не имеют значения в этом контексте.

Я бы предложил начать с построения графика этой функции из ваших данных (не того, что с фиксированным $n$, а того, который отображает $n$ на оптимальное значение $p$). Было бы полезно узнать, как он выглядит, в особенности для выбора подходящего метода регрессии.

[редактировать] О работе с шумом.

Стандартный статистический способ работы с шумом — ничего не делать 🙂

Сколько у вас данных? Потому что если у вас достаточно данных, статистически шум должен уравновешивать сам себя. Например, если у вас есть 100 таких графиков для фиксированного $n$, среднее оптимальное $p$ должно быть достаточно близким к истинному оптимальному $p$. Даже если для некоторых значений $n$ данные не содержат оптимального значения $p$, по мере увеличения значений $n$ этот шум вряд ли будет значительным. Важно, чтобы модель регрессии правильно представляла общую тенденцию, а не захватывала небольшие вариации, вызванные шумом.

Я бы начал с графика, состоящего из одного ящика диаграммы для каждого значения $n$ и варьируемого $n$, где множество значений, представленных в ящике диаграммы, — это все минимальные $p$ в данных для этого значения $n$.

[редактировать 2] Еще одна интересная визуализация: вы можете представить свои полные данные в виде тепловой карты, где $n$/$p$ находятся на осях X/Y, а цвет основан на значении $f(n,p)$).

Поскольку вы утверждаете, что аномальные значения следуют особой модели, одним из вариантов является удаление всех значений, превышающих порог изменения. Порог изменения может быть установлен вручную или изучен. Другими словами, составьте правило, основанное на первой производной от реализованных значений данных.

Вот пример на Python:

time_all = [.8, .7, .6, .5, .4, .3, .2, .1, 0, .2, 0, 
            .2,  0, .1, .2, .3, .4, .5, .6, .7, .8]
change_threshold = .15        

time_valid = [time_all[0]]
for t0, t1 in zip(time_all, time_all[1:]):
    if (t0 - t1) < change_threshold:
        time_valid.append(t1)